Curly

My MIG-15 SFM mod might not provide an entirely suitable analog for a MIG-17, as there are some significance changes between the two aircraft that effect performance. I'll highlight some of these changes and their effects with diagrams from the MIG-15 and MIG-17 Technical Manuals. The MIG-15 Data will have white back grounds. Like this basic profile and size drawing of the MIG-15Bis null The MIG-17 diagrams will all have a black background this. On the MIG-17 there were significant changes to the wings, in terms of both airfoil, area and sweep angle. For instance the MIG-15's wings are swept at a 35 degrees angle The wings on the MIG-17 are swept at an angle of 45 degrees The combine effect of the changes of airfoils, wing area and wing sweep angle, resulted in significant changes to the lift and drag profile of the MIG-17 Vs MIG-15. Compare the MIG-15's Lift and drag polar at Mach 0.2 To that of MIG-17's The Cy / (CL) max of the MIG-17 is lower than the Cy / (CL) max of the MIG-15. The profile of the lift curve , what's called Cy_Alpha in the SFM, (Cy per AOA) also differs between the MIG-15 and 17. The MiG-15 Cy / Alpha Compared to the MiG 17's At high mach numbers the advantage of the MIG-17's wing profile is apparent. While at lower mach numbers the MIG-15 requires less AOA for a given lift coefficient. These changes were a result of design decisions made to optimize the performance and handling qualities of the MIG-17 at high mach numbers. Comparison of the drag profile of the MiG-15 and 17 also high lights the desire to improve aircraft performance at high mach numbers. Compare the MiG-15's high speed drag profile. To the MIG-17's Given both turn and climb performance can be quantized as functions of ( CL / CD ) * ( T / W ). Changes to weight of the SFM MiG-15 alone may result in under and over performance of a MiG-17 at high and low mach numbers. I haven't sat down with a spreadsheet and computed the performance of the MIiG-17 the way I did with the 15 though. So I can't tell you how much of difference in aircraft performance a more through approach to a MIG-17 SFM flight model would make compared to just changing the weight of the MIG-15. However, examination of the Thrust Required Vs Thrust Available charts may provide some insight into the matter. As the difference between thrust required Vs thrust available, being fundamental to both sustained turn and climb performance. MIG-15Bis Thrust Available Vs Thrust Required MIG-17 Thrust Available Vs Thrust Required.

I've been keeping the MIG-15 Bis SFM mod updated locally. I never bothered to post the files because I didn't think anyone was really using it. I've placed the mod on Git Hub so that anyone can easily inspect the changes. https://github.com/AeroBaseAlpha/DCS-MiG-15bis-SFM-Overhaul/blob/main/CoreMods/aircraft/MiG-15bis/MiG-15bis.lua

Just as an FYI, The dispersion doesn’t scale linearly with Da0. Nor does Da0 = 100% dispersion. In short, Da0 and the 80% diameter circle represent two different ways of describing the probability density functions of dispersion. Da0 is not a measure of radial dispersion. Though it is possible to convert Da0 to a measure of radial dispersio. The 80% diameter of dispersion is = to Da0 * 5.3199. If we set Da0 to = 0.00495. The diameter of 99.7% circle would be 50 mils, filling the F-5E’s gunsight At the bottom of this post,I’ll further explain the difference between Da0 and measures of dispersion commonly used in the west, like 8 mil 80%, Before we examine the recent changes to the dispersion I would First like to establish that the 8 mil 80% dispersion rating of The F-5E guns, represent the diameter of a circular pattern. This is made clear in the F-5E Weapons Delivery Manual F-5E-34-1-1 1 Aug 1979 , rev 1980. On page 223 under the boresight section. Where it states the acceptable dispersion pattern for the M39’s on the F-5E is a 8 mil circle which contains 80% of the rounds fired. The 80% diameter of dispersion can be described mathematically as being = sigma * sqrt(-8*ln(1-.80)). Where sigma is the standard deviation of the dispersion. Based on one the devs comments, https://forum.dcs.world/topic/207864-closed-m61-dispersion/page/2/#comment-3916757 The DCS dispersion parameter, Da0, is equivalent to a median dispersion. This is commonly called Range or Deflection Error Probable in the west. Da0 / REP is also a function of the standard deviation of dispersion, Where Da0 is = 0.6745 sigma. We can convert the dispersion rating in the F-5E manual, 8 mil 80%, to (Da0) with some simple math. We just multiply the 80% circle rating, 8 mils by 0.18797 to get Da0. Which would make Da0 = to 1.5038 mils. In the proper format for the game, Da0 should = 0.0015. Before the update, Da0 was = 0.0022 This resulted in an 80% diameter of 11.7 Mils. The old dispersion was about 46% larger than indicated in the F-5E’s manual. With the latest change Da0 was reduced by about 27% to Da0 = 0.0016 The current setting should result in a 80% dispersion diameter = to 8.5 mils. Which closely matches the data given in the manuals Below we’ll look at an old dev post on dispersion and I’ll explain the difference between Da0 and the type of dispersion ratings often given like, 8 mil 80%. Per the dev, Yo-Yo, about 8 times the dispersion variable, Da0, will give you the diameter of the 100% dispersion circle. https://forum.dcs.world/topic/207864-closed-m61-dispersion/page/2/#comment-3916757 The implication is that Da0 is not a measure of radial dispersion. Da0 represents a normally (Gaussian) distributed univariate measure of dispersion which contains 50% of dispersion along the x and y axis separately. In western technical literature, Da0 would be equivalent to what is known as Error Probable, Range Error Probable Or Deflection Error Probable. Da0 / REP are = to 0.6745 * the standard deviation of the dispersion (sigma) In most western literature the dispersion is given as either a radius or diameter and a probability, like 80 mils 80%. Circular Error Probable or CEP is another commonly used measure. CEP is the radius of a circle which contains 50% of the impacts. CEP is = 1.17741 * sigma. Note that CEP and REP / DA0 do not have the same relationship to the standard deviation of the dispersion ( sigma). This is because CEP and dispersion ratings like the 80% circle are functions of a different probability distribution than Da0 / REP. If bullet dispersion is circular normal. Then sigma x and sigma y are equal. We can describe the radial dispersion as a function of sigma. With the equation sigma * sqrt(-2 *ln(1-% radius of dispersion) For example the 75% circle is given as; The radius of 75% circle is = sigma * sqrt(-2 *ln(1-0.75) Or sigma * 1.6651 is = the radius of the 75% circle of dispersion. CEP aka the 50% radius of dispersion is = sigma * sqrt(-2 *ln(1-0.50) Since sqrt(-2 *ln(1-0.50) is = 1.17741 then, Sigma * 1.17741 is = to the 50% radius of dispersion. Lets compute the 50% radius of dispersion base on the on the F-5E dispersion value Da0. The most straightforward way to do this is to compute sigma from the DCS dispersion parameter. Given that; Da0 = 0.0016 = sigma *0.6745 Then sigma is = (0.0016)/0.6745 Sigma = 0.00237 = 2.37213 mils Since the 50% radius dispersion is = sigma * 1.17741 The 50 % radius of dispersion, CEP, is 2.79297 mils As, 2.37213 * 1.1774 = 2.79297 mils.

Some parameters on the MiG-15bis guns do not match the historical data. These errors tend to reduce the effectiveness of guns. I’ve created a mod to match the historical data as closely as possible. You can find a link to that here. Of particular concern are the dispersion values and weights of the projectiles in DCS. Perhaps some of these proposed changes could make it in before Flaming Cliffs 4 comes out. https://www.dropbox.com/scl/fo/0vg8jko4cdn5dsfx4k3ri/AFeR-Qst2XAl69xxI6Wx_LY?rlkey=vevkaqfqxvt4hkw3k0pxyekyq&st=5dcqhkr1&dl=0 Of particular concern are the dispersion values and weights of the projectiles in DCS. The proposed changes to the bullets are: 23MM HEI-T 23MM API 37MM HEI-T 37MM AP-T Dispersion Old 0.0007 0.0007 0.0017 0.0017 Dispersion New 0.0012 0.0012 0.00083 0.00067 Bullet Weight Old 0.196 0.199 0.722 0.765 Bullet Weight New 0.196 0.199 0.735 0.753 Filler Weight Old 0.011 0 0.41 0.41 Filler Weight New 0.014 0.006 0.041 0.008 Tracer Off New 2.5 2.5 3 3 life_time New 8 8 8 8 The 23MM and 37mm should also be changed to match the data from the historical data. Those proposed changes are: NR-23MM N-37MM Rate of fire Old 850 400 Rate of Fire New 860 400 Ratio of HE/API in Gun Belt, Old Ratio 2 HEI-T / 4 API 2 HEI-T / 4 API New Ratio 5 HEI-T / 2 API 5 HEI-T / 2 API The proposed values correspond to data from official documents. The primary sources are: The Soviet Technical Manual for Aircraft Guns https://disk.yandex.com/i/YVj0XI6O3Mu4LM MiG-17 The Flying Techniques and Combat Manual: Link below https://annas-archive.org/md5/bd31e5163d094e0ba055e8dccaaa0a0c Volume of 2 of Technical Manual for the MiG-15bis: Armament. Evaluation of Soviet Automatic Aircraft Guns 37mm NS and 37MM N 1952 Link: https://apps.dtic.mil/sti/tr/pdf/AD0004232.pdf The change are discussed in detail below 37MM The dispersion is too large on the N37 HEI-T. Currently Da0 is set to 0.0017 The weapons manual indicates the mean error is 0.5 meters at a range of 600m The appropriate value for the DCS N37 HEI-T is = 0.5 / 600 or 0.00083 In DCS the mass of projectile is off, It’s 0.722 kg and should be 0.735 kg The weight of the explosive in DCS 37MM HEI-T is 100 times greater than the data from the technical manual. In DCS the charge weighs 0.410 kg. The weight of the HEI charge in the real shell is 0.037kg. The weight of the tracer chemical is 0.008 kg. So max weight of explosive should be between 0.041 or 0.037 in DCS. The tracer in DCS also turns off too early. In DCS it shuts off after 1.5 seconds. Based on the time of flight of the projectile from the American evaluation. The DCS tracer turns off after traveling 1000 meters, 500 meters short of the burn distance given in the Russian Aircraft Weapons manual on page 47. From the previous TOF chart. We can estimate the TOF at 1500 meters to be around 2.5 to 3 seconds. So I’ve set tracer_off to = 3 for both the APT and HET projectiles. Given the duration of the tracer burn, I believe the life time of the projectile should be increased to at least 8 seconds. In DCS the projectile life time is set to 5 seconds. Thus after 5 seconds the DCS bullet explodes. The manual does not indicate there is a self destruction feature on this shell. So the lifetime of the bullet should be greater than the burn time of the tracer. 37MM APIT The dispersion is also too high for the 37MM APIT shell in DCS. In DCS the dispersion value Da0 is set to 0.0017. That value corresponds to a probable error of 1.02 meters at 600 meters. The Soviet Manual notes the largest acceptable probable error at 600 meters is 0.4 meters. Thus, the appropriate value for Da0 is = 0.4/600 or 0.00067. Similarly to the DCS 37MM HEI -T, The API-T tracer turns off too early, at 1.5 Seconds. It also self-destructs after 5 seconds. Based on the time of flight of the projectile, Both the tracer duration increased to 3 and the projectiles lief time to 8 seconds. 23MM Bullets: The dispersion in DCS is too low for both 23MM projectiles the MIG-15bis fires. The dispersion for both, the API and HEI-T, is Da0 = 0.0007. The DCS version of these bullets have a probable error of only 0.35 meters at a range of 500 meters. The actual dispersion for these bullets was 1.714 times larger. As the Aircraft weapons manual gives the probable error as 0.6 meters at 500 meters, Da0 should be = 0.6/500 or 0.0012. An increase in the dispersion will likely improve the effectiveness of the 23MM in game. An appropriate amount of dispersion keeps a lethal density of projectiles down the entire range of the sight line. As indicated by the MiG 17 Combat Manual, the designers at the BBC optimized the sight setup to account for this. The sight was angled downward to account for the angle of attack at the assumed optimal firing parameters as well. Given the 50 meter boresight target in the Armament Technical Manual for the MiG-15bis is identical to the one in the MiG -17 Combat manual. We can assume that, the MiG-15bis sight and weapons are angled the same. Above MiG 17 50 meter boresight target. Above: MiG 15bis 50 meter boresight target. For the 23MM HEI shell I also increased the weight of by 3 grams to account for the tracer material. As the tracer substance can have an incendiary effect. A payload of 0.006 kg of incendiary was added to the 23mm API. As the real projectile contains 6 grams of incendiary agent. The tracer time for the 23MM HEI-T was increased to reflect the tracer length of 1200 meters given on page 34 of Soviet Aircraft Weapons and Bullets manual. The current trace duration is 1.5 seconds and seems low based on the ballistic tables for similar projectiles. I’ve set changed to 2.5 seconds based on the ballistic tables for the 23MM Vya For comparison, The HEI fired from 23MM VYa cannon with a muzzle velocity of 890 mps takes 1.81 seconds to travel 1200 meters. Given the lower muzzle velocity of DCS projectile, the tracer is likely to burn out before it travels 1200 meters. We can use this table to estimate the tracer burn time for MIG-15’s 23MM HEI-T bullet. The velocity of the VVY projectile at 600 meters (675mps) is comparable to muzzle velocity of MIG-15’s HEI-T (680mps). If the firing table listed the time of flight to a range of 1800 meters. We could have used the TOF’s to 600 and 800 meters as the duration of the tracer lifetime. As the Tof 1800 - TOF 600 = TOF over 1200 meters = Tracer burn time. However, the chart only goes to 1200m meters. We are forced to make an estimate of the TOF to 1800 meters. We’ll do this by examining the rates of change of the TOF and the change of this change. Thus we estimate the TOF to 1800 meters as ~ 2.95 seconds. As the TOF to 600 meters is 0.774. We compute the tracer burn time as 2.2 second, as: TOF 1800 - TOF 600 = Tracer Burn Time 2.98-0.774 = 2.21. We can assume this estimate is somewhat accurate, as the projectile stays within the linear part of the mach drag curve. Thus a tracer burn time of 2.5 to 3 seconds seems reasonable. The ammo belts of all the guns have been changed to a mix of 70% HEI and 30 API. Which are the proportions given in the MIG-17 Combat Manual. Currently the NR23 fires belt consisting of 2 HEI and 4 API. The N-37 fires 3 HEI and 1 APIT. I chose to implement a ratio of 5 HEI and 2 API on the 23MM and 37MM. This makes the ratio of HEI to API equal to 2.5. Close enough to the ratio given in the manual 70/30 or 2.333. To ensure both 23MM cannons do not fire a tracer at the same time. The placement of the tracers is 23MM cannons are different from one another. These changes are made at line 375 in the lua file in the Guns table. The rate of fire of the cannon was changed in this section of the LUA to. The ROF of both cannons is offset by +-1 RPM. DCS doesn’t always deal with two guns with same rate of fire on the same aircraft. The RPM offset mitigates this. The rate of fire of the 23mm cannon was increased to 860 rpm. 860 being the mean rate of fire given in the MiG-15bis Technical Manual Volume 2 Armament. The variable which controls the range at which the AI will open fire, tbl.effective_fire_distance,was also changed of both the 37mm and 23mm cannons. It was reduced from 1000 meters to 600 meters. 600 meters was chosen based on the effective range of the weapons and sight system as described in the MiG-17 The Flying Techniques and Combat manual. As a result of this change, the highest skilled AI will only open fire at 600 meters or less. The lowest skilled AI will begin shooting at approximately 420 meters. These values are based on the notes in \Scripts\AI\Skill_Factors.lua. CANNON_FIRE_DISTANCE_COEFF = 29 --effective fire distance = fire distance * fire distance coeff The value of lowest skilled AI is set to 0.7 and the most skilled is =1 [CANNON_FIRE_DISTANCE_COEFF] = 0.7, For testing purposes, I’ve disabled the barrel heating mechanic by setting shot to 0 on all the guns. This was done to verify the accuracy of the dispersion changes. It may also be worth considering reducing the recoil coefficient on all the guns. The magnitude of the effect seems overdone, shaking the aircraft considerably when firing. While the N37 is a large weapon with considerable recoil force, it does have a muzzle brake to reduce these forces. The recoil effect is governed by the parameter, recoil_coeff. It is currently set 1 on both guns. At 0.5 the forces are reduced considerably. When computing the recoil force DCS only seems to consider the projectile mass and the muzzle velocity, whatever other transforms it applies . If you made it this far, Thanks for taking the. Please let me know if you have any question or concerns.

I'm working on a post about the weapons right now. RE: The accuracy values of the weapons: The DCS parameter for dispersion, Da0. Is equivalent to Range Error Probable or 0.6745. the standard deviation of dispersion (sigma). The radial dispersion values often given in western literature are also functions of the standard deviation of dispersion (sigma), assuming circular dispersion. The radius of the 80% circle is = sigma * 1.7941 As, (sqrt(-2*ln(1-0.8))) = 1.7941 To convert the DCS value of dispersion, Da0, to the 80% radius of dispersion: Da0 * (1/0.6745) * 1.7941 = The radius of 80% of the dispersion or The radius of 80% dispersion is = 2.66 * Da0. With this method we can compute the 80% radius of MIG-15 weapons in DCS and from the manual as: Projectile: DCS 80% Radius 80% Soviet Radius N-37 HEI 4.5219 2.2166 N 37 APT 4.5219 1.7733 23 mm 1.8620 3.1919 M61A1 4 50 Cal Aircraft 2.153 The increased dispersion of the 23MM cannons is probably going to improve the effectiveness of the weapons. Some dispersion is necessary to compensate for errors in fire control equipment and can reduce penalties for aiming error. To much Dispersion and the density of projectiles within the target drops. Which reduces the overall effectiveness of the system. The Soviet practice was to maximize the effectiveness of the weapons for a specific size targets over an the effective range of the weapon system. See the image below. The dispersion of the projectiles on the MiG-15 and 17 appear to optimized for their specific use cases. The 23MM being used to target fighters. The increased dispersion and rapid rate of fire would be ideal for engaging fighter sized targets at close ranges in high G maneuvering. While the 37mm would be more ideal for shooting at large non maneuvering bombers from long range.

Problem: The AI controlled MiG-15bis has unrealistic performance. Cause: Some of the aerodynamic characteristics of the SFM exceed those of the real aircraft. If we compare the SFM data in MiG-15bis.lua to the aerodynamic data from the real technical manual for the MiG-15bis. https://www.digitalcombatsimulator.com/en/files/2365583/ Some discrepancies are apparent. For example, the DCS MIG-15Bis SFM has 200 kgf more thrust than the real MiG-15 bis at low speed. This is because the thrust values for the SFM are based on bench tests of the VK-1 Engine and not on installed thrust data. The installation losses are given in Figure 84. The manual confirms this and notes figure 80, reflects these losses. Since thrust available defines many of the performance parameters of the aircraft. It is important that the SFM thrust parameters match this data. Using the data from the technical manual, I’ve updated almost all of the SFM of the MIG-15bis to more closely match the real aircraft. Feel free to try it out, I’ve placed a link below. The mod contains extensive notes. I cite a source for almost every change I’ve made to the SFM too. Link to Mod: https://drive.google.com/drive/folders/19cQXcBNfOdnoJkxlY2BFdUO3Zc77KESm?usp=sharing I’ve tested and validated the performance of this mod in a few different ways too. The max velocity at various altitudes, climb rates as given in table 5 of the technical manual. The SFM also matches the level acceleration data in figures 46. Below I’ll discuss some of the changes I’ve made to the SFM to more closely match the historical data below. Almost all of the aerodynamic table was changed to better match the source data. Drag: The drag polars Cx = Cx_0 + Cy^2*B2 +Cy^4*B4 Were changed to better match figures 55 and 54. A new data point was also added at mach 0.86. Which is important because the lift and drag become nonlinear here due to mach effects. LIFT: Cy max as function of Mach was changed to match Figure 185. The current values in SFM are too high, resulting in too much lift. The SFM Cy max values are drawn below in red, The mod’s Cy max are drawn in the green line. Cy Alpha was also changed to more closely match the actual aircraft. Cy0, the zero AOA lift coefficient, was set to match the lift polar in figure 51. Aldop was set to the AOA corresponding to CY max from fig 185 and Cy alpha at that mach. AOA = ((1/Cya)*Cy+((Cy0*-1)/Cya)) Engine: Some additional changes were also made to the SFM engine model. Dpdh_m was changed to more closely match the loss of thrust as a function of altitude. Thrust Kgf At Alt = Thrust Base (Kgf)-(dpdh*(Alt m*0.001) Above, the thrust available at 5000 meters for SFM is drawn in red. The mods values are drawn in blue. At low speeds the mod more closely matches real aircraft. The mod also changes to the idle rpm and thrust specific fuel to more closely data in table 19. Roll Rate: Omxmax, the max roll rate was changed to match Figure 40: Other Changes and Notes: V_opt = 367 / 3.6, -- velocity for L/D Max, Mach .3 at 0 m =367 TAS Kph Page 24 . Setting V_opt to high means the AI does not have enough excess thrust to maneuver. causing it to only do high speed loops. V_cruise = 1.31*V_opt .Def of Vopt from translation of Russian Aircraft Design book. https://archive.org/details/DTIC_AD0741485/page/62/mode/1up g_suit = 0.0, -- This Aircraft does not have a G suit, Default is 0.35, AI will sustain 6g turns all F-86 = 0.7 -- Performance Limiting Factors of AI SFM are AI Level, Cy Max, drag, Aldop, and g_suit, Vopt CAS_min = 50, -- This is Close Air Support time on station in Minutes. How long (the AI) will LOITER TIME, WEAPON CHANGES There are also some changes to the weapons parameters. I plan on doing a separate post on these changes. One of the most impactful of these changes was changing the value Tbl.effective_fire_distance to 600m to reflect the data on the 23mm and 37mm cannon uses as presented in Table 18 in The Flying Techniques and Combat Use of the MiG-17 Which gives the effective ranges when firing at fighter aircraft as 180 to 550 Meters. The previous value was 1km and resulted in a sniper bot. There are also changes to dispersion values, shell and fillers weights. These changes were made to match the data from Soviet Manual on Aircraft projectiles. https://disk.yandex.com/i/YVj0XI6O3Mu4LM That just about covers all the changes I’ve made to the MIG-15bis SFM. While these changes are not a miracle fix for the AI or the SFM. I feel the do represent a significant improvement to the AI MIG-15bis making the AI MiG-15 a much more realistic and engaging opponent. I believe this project illustrates that significant improvement to the AI performance can be made if one takes the time to realistically tune the SFM parameters. With a spreadsheet and an understanding of the SFM parameters it’s possible to create much more realistic SFM AI opponents. Eagle Dynamic could also do a lot to improve the situation by better explaining the SFM parameters. Many of the notes in various SFM files date back over a decade and are from unofficial sources, some are misleading others are simply incorrect. If you read this far, thanks for taking the time to do so. If anyone wants it, I will share the google sheet I used to help develop this MOD. Be forewarned though, it’s a hot mess and some of the units are in …Gasp! American units of insanity. I attached a track of a big dog fight mission, sabres V Mig15's down low. I know it's need for the report. Thanks for taking them time. MIG 15 Big Gun Fight.trk

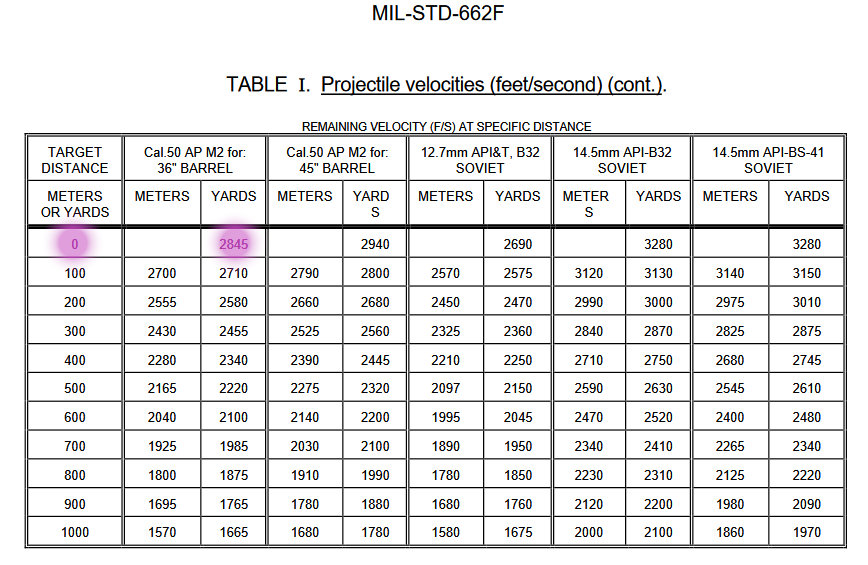
The firing table for the M8 AP is for the 28 lb 45 inch heavy barrel machine gun. The firing tables the Air Force manuals are based on the 10 lb 36 inch aircraft machine gun barrel. the reason for the difference in between the two manuals is because heavy barrel is less prone a drop in muzzle velocity than the light M2 barrel. Given the same burst length the barrel of the lighter 36 inch aircraft expands more and the overall temperature of the 36 inch barrel is greater. Resulting in a greater reduction in velocity and accuracy for the 36 inch barrel. The 28 lbs heavy barrel can fire 8 times more rounds Compared to 10 lbs 36 barrel used on aircraft machine guns. The reason for the difference in between the two manuals is because heavy barrel is less prone a drop in muzzle velocity than the light M2 barrel. If you want some direct proof that the cold barrel muzzle velocity of a 36 inch aircraft machine gun barrel firing M2 AP has a muzzle velocity of 2845 fps I'll point you to the firing tables in MIL STD 662.

The firing tables for field use, like AAF manual 200-1, use reduced muzzle velocities for their tabulations because they are accounting for wear and the average velocity of the bullets in a burst. This is plainly stated in M8 API ballistic table. The ballistic data in those AAF field manuals. Often comes from firing tables like the one above, FT 0.5AA-T1. In “AAF-200-1 Fighter Gun Harmonization” The data comes from Aberdeen Firing Table FT. 50 AC M-1 https://archive.org/details/aaf-manual-200-1-fighter-gun-harmonization/page/9/mode/1up The ballistic data in “Air Force Manual 64 Fighter Gunnery” Comes from FT. 50 AC-M-1-8 https://archive.org/details/air-forces-manual-no.-64-fighter-gunnery-firing-rockets-dive-bombing-1-may-1945/page/111/mode/1up The reduced muzzle velocity (2700 FPS) used in AAF-200-1 is representative of a gun halfway through its service life. The Army Air Force considered a 50 caliber machine gun barrel worn out when the cold gun muzzle velocity of the weapon dropped by 200 fps. https://archive.org/details/hypervelocitygun01bush/page/466/mode/1up However, If you want some more sources with higher muzzle velocities from the war with. I can provide a few more. There’s TM 9220 It gives the muzzle for the M2 AP from the 36 inch aircraft machine guns as 2845 fps The same document gives the muzzle velocity for the M1 Incendiary when fired from the 36 inch aircraft barrel as 3,100 fps https://archive.org/details/TM9-2200/page/n209/mode/2up Or the 1944 version of “Terminal Ballistic Data” Which contains the Range, impact velocity and armor penetration values for the 50 Caliber AP M2. The test from the Ballistic Test Section was conducted on December 20 1943. This report gives the muzzle velocity of the 50 Caliber M2 AP as fired from a 36 inch aircraft barrel as 2845 fps. The 1945 Version of this same report gives the muzzle velocity as 2,835 fps. Including the data sheet. and The revised Velocity Penetration Graphic. Or From the Small arms R and D report. Which states the muzzle velocity at 78 feet from the 36 inch barrel is 2810 fps. When you take in the totality of all source materials and account for the practical application of the use of the firing table. I feel it safe to say that muzzle velocity of the 50 caliber projectiles, fired from a cold barrel, is best represented by the values in the 1946 Technical Manual for 50 Caliber aircraft Machine gun. The 2700 fps value, used in the Air Force firing tables already accounts for reduction in muzzle velocity due to burst firing and wear. When the game applies additional reductions in muzzle velocity with the shot_heat effect, it's over modeling the drop in velocity. The drop in velocity due to burst firing is baked into the Air Force firing table. The procedure for accounting for the drop in muzzle velocity due to burst fire when the firing table is created, is described by the Agency which creates those tables, The Ballistic Research Lab. In BRL Report 889 "On The Computation Procedures for Firing and Bombing Tables" https://apps.dtic.mil/sti/tr/pdf/AD0027123.pdf I know that you can ruin the performance of a 50 caliber machine gun by burst firing it. I’m not advocating for turning off shot heat for these weapons. I’m well aware that a continuous burst of 170 bullets will reduce the velocity life of a standard steel M2 50 Caliber Aircraft to zero. https://archive.org/details/hypervelocitygun01bush/page/481/mode/1up Meaning that weapon would fire 200 fps slower than a new 50 caliber, EG a worn out barrels fires around 2600 fps from a cold barrel. As this was the definition of the velocity life of the weapon. https://archive.org/details/hypervelocitygun01bush/page/466/mode/1up Velocity drop and an increase in Dispersion should be in game. However the 50 caliber machine gun DCS models is half worn out and and prone to to delivering muzzle velocities for a weapon closer to the end of its service than the begging of it . I would make this same argument for why a small reduction in the dispersion value is important. When the heat effect is added to the slightly larger dispersion, the dispersion is too great and over modeled. Again, I’m not trying to argue that burst firing should should not increase the dispersion of the projectiles. I’ve read detailed reports on how long of a burst fire it takes to reduce the accuracy of this weapon https://archive.org/details/hypervelocitygun01bush/page/466/mode/1up And The effect burst length can have on accuracy. I chose to use the 1.2 milliradian std deviation as the basis for my mod because that value is so widely used in various manuals. 4 mil 75% Shows up over and over again in numerous Air Force Weapon manuals. And It continues to show up after the war too. 4 mil 75% / 8 mil 100% was still the standard in the 1950’s https://www.google.com/books/edition/AF_Manual/81krAQAAMAAJ?hl=en&gbpv=1&pg=PA155&printsec=frontcove The fact that this figure was used over and over again for as long it did gave reasonable assurance that this was a sound basis for an accurate assessment of the gun's accuracy. There was also some other data in form of mean radius that I chose not to use because, if you computed a standard deviation for the mean radius given It was far below what the Air Force was using in their manuals. It looks like they may have had switch the notation of feet with inches when they wrote the mean radius. The document also does not define mean radius. Is it CEP? Error Probable? the Mean Radial Miss distance?. There were just to many questions about the data in this table. So I did not use any of these figures as the basis for my mod. https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13265 I just want to impress upon you the level research and consideration that I put into developing this mod. I didn't just pick the best numbers. I selected numbers which would best represent the cold barrel performance of new 50 caliber M2 Aircraft Machine Gun. Is this the report you based your accuracy data on? Or was it that Russian P-40 firing test I've heard about but have never been able to get my hands on. I appreciate that you looked at this and I hope that I have convinced you to take another look at the data presented.

In the hope of creating further discussion on this topic. I’ve created a “Historically Accurate 50 Cals Mod”. The mod changes the 50 caliber the muzzle velocity, projectile weight, filler weight, dispersion rating and tracer off times where appropriate, to match the historical data. This mod will only affect the aircraft and vehicles which use the WW2 50 caliber ammunition. So the P-51, P-47, ect. Aircraft, like the F-86, which use their own unique implementation of the Browning 50 caliber will not be affected by this Mod The mod is provided in a format that is compatible with the mod managers JSGME, OVGME. Using a mod manager allows you to easily toggle the mods on and off without ruining the base DCS install. Link to the Mod Below. https://drive.google.com/file/d/1dAMiOFVFmrIZQq_LtjGD-S9PsMn3z9Uz/view?usp=sharing Below is a table comparing the characteristics of the various DCS 50 caliber projectiles and those in the mod. The Mod In Detail: Due to my previous research, I’ve been able to create a mod which accurately simulates the various 50 caliber projectiles to an incredible level of detail and historical accuracy. Everything down to the tracer burn time is based on primary source materials. Below I’ll discuss all of the changes this mod makes to the various 50 caliber projectiles and provide source materials and links justifying those changes. Fair warning, things get a math heavy at the end, the dispersion section in particular. If you have any questions or comments feel free to reach out, I’m always happy to explain something. With that out of the way, let’s begin going through the changes this mod makes to the 50 caliber projectiles Muzzle Velocity: The muzzle velocity of the modded projectiles are from the 1947 version of the 50 Caliber Aircraft Machine Gun technical manual. “War Department Technical Manual, TM-9-225 Machine Gun technical manual for the Browning Machine Gun Caliber .50 AN-M2 Aircraft, Basic.” January 1947. The Manual is available on Google Books. https://books.google.com/books?id=nXySRue3QAYC&pg=PA170#v=onepage&q&f=false The muzzle velocities within this manual are the most commonly occurring values throughout the technical literature. These values are also representative of the true muzzle velocity of the bullets when being fired from the cold bore of a new gun. Therefore the muzzle velocities within the Weapon’s Technical Manual are reasonable to use as the DCS variable v0 which is equivalent to cold bore muzzle velocity in meters per second. Projectile Weight and Filler Weights: The mod changes projectile weights and payload weights of the DCS projectiles to match the weights from the projectile blueprints / schematics as presented in the Ordnance Departments Official Research Record of Small Arms and Small Arms Bullets Research and Development Report. The Official Ordnance Department’s Report is the best source for this type of information. The Ordnance Department oversaw not only weapons R and D, but also supervised the manufacture and testing of these projectiles throughout the war. The drawings / schematics of the projectiles were updated throughout the war to reflect various changes in design that occurred during the war. For example The M1 incendiary design was submitted in 1941 and was revised 10 times by 1945, the schematic was updated accordingly. Given the origin of these schematics and their continual reversion. The Ordnance Department's Report and drawings are the best source for projectile and payload weight. If you skipped down to look at the schematics, some of you may have noticed that Some of the projectile drawings have two weights listed. The M8 API for example During the war, the Tungsten Chromium core was replaced with a lower weight hardened steel core. page 190 of the Army Ordnance Research and Development Report for Small Arms Ammunition. 1946. https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13268 Therefore the weights of the Modded projectiles are equal to those of Alternate core versions. As the alternate core 50 caliber ammunition would have been in use during World War 2. Below, In the spoilers, are the blueprints for the 50 Caliber Projectiles effected by this mod. The design drawings all come from various parts of the “Army Ordnance Small Arms Ammunition Development Report” The only link I can provide to this document is from The Archive of the Small Arms Review. The report is split into 6 parts, all of which can be downloaded for free. Link to Part 1: https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13265 Blueprint M2 AP Blueprint M8 API Blueprint M20 APIT Blueprint M1 Incendiary Blueprint M1 Tracer The weight of the incendiary payload in the mod, is equal to the weight of the incendiary payload + half the weight of tracer composition. The M 20 APIT has a payload of 18 grains of incendiary and contains 14 grains of tracer. Thus the payload of the M 20 APIT in the mod is 25 grains, as 18 + (14*0.5) = 25 grains or 0.0016 kilograms. Tracer Burn Times: For the M1 Tracer, burn time is directly from from The Ordnance R and D report. The M1 Tracer burns for 3.8 seconds. Therefore, the mod sets the tracer off time to 3.8 seconds for the M1 Tracer. Determining the appropriate trace off time for the M20 APIT is a bit more complicated. As I could not find an exact tracer burn out time for the M20 APIT, only the specified burn distance. So we’ll have to compute the time of flight to burn out distance. Warning there be maths below! The Ordnance Department’s Research And Development Report on Small Arms Ammunition Tracers does give the length of tracer burn. The Tracer is expected to burn over 1800 yards. https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13266 A footnote in M2 50 Caliber Machine Gun’s technical manual gives a similar burn out distance. In DCS we specify the burn out time of the tracer. If we want the mod to match the historical data, we just have to compute the TOF of M20 APIT to 1800 yards. Then set the tracer on M20 APIT to turn off when the bullet has flown 1800 yards. As the goal of this mod is historical accuracy. When we compute the time of flight to 1800 yards, We’ll use the same methodology the Ballistic Research Laboratory employed to compute firing tables during World War 2. This computed TOF to 1800 yards will be the number of seconds DCS waits before turning off the tracer effect. The analytical technique used to compute firing / ballistic tables is explained in detail within the National Defense Research Committee report “Analytical Studies in Aerial Warfare”. https://archive.org/details/analyticalstudie02bush/page/12/mode/1up Putting the time of flight equation into something a bit more manageable we get. TOF= (1/((V0/Range)-((.00372*rho)/(2*BC)*Sqrt(V0))) Where V0 = The Bullets Muzzle Velocity + The Aircraft Speed (TAS) In FPS, We’ll set V0 to the muzzle velocity of M20 APIT, when being fired from a stationary position on the ground, from an M2 machine gun with a 36 inch aircraft barrel. The Technical Manual for the 50 Caliber M2 Caliber Aircraft Machine gives the muzzle velocity of M20 APIT as 2950 fps. V0= 2950 (fps) C5 is the C5 ballistic coefficient of 50 Caliber M20 APIT, This value is = 0.437 As is stated in BRL Report Form Factors of Projectiles. https://apps.dtic.mil/sti/pdfs/AD0802080.pdf C5 = 0.437 Rho is the relative air density to the sea level standard ballistic density 0.07513 lb / feet^3. This is also called the density ratio. At sea level, on a standard day, this value is 1. Rho =1 The Range is 1800 yards, however this equation uses feet as the format for the range input. So we just convert yards to feet and Range is set to. Range = (1800*3) The NDRC equation configured to compute the TOF to 1800 yards for the M20 APIT now looks like: TOF = (1/((2950/(1800*3))-((.00372*1)/(2*0.437)*Sqrt(2950))) Thus TOF To 1800 Yards = 3.173390047 Seconds. Let's compare our computed TOF to some historical data and see if the NDRC time of flight equation we used is accurate. We’ll look at a Ballistic table for the M8 API from 1946. Given that, the M8 API is a ballistic match to the M20 APIT . if we correctly set up the NDRC TOF equation and compute the TOF of the M8 API to 1800. And, the computed TOF is equal to the TOF data within the real Ballistic / Firing table. We can reasonably assume that the computed TOF of the M20 APIT is accurate. This Firing table is for an M8 API fired from a 45 inch heavy barrel version of the 50 Caliber Browning, with a muzzle velocity of 3000 fps The ballistic table says the time of flight to 1800 yards is 3.08 seconds. Now we just have to configure the NDRC TOF equation with the proper variables for the M8 API. If the computed time of flight to 1800 yards is close to 3.08 we can assume this equation is accurate enough for our mod. To configure the TOF equation to compute the TOF of M8 API to 1800 yards. We change the muzzle velocity to be equal to the muzzle velocity in the ballistic table. Meaning we set V0, to 3000 fps V0 =3000, We also have to change the C5 ballistic coefficient the correct value for the M8 API, which is 0.439 https://apps.dtic.mil/sti/pdfs/AD0491936.pdf BC M8 API = 0.439 The range is still = (1800*3) feet The time of flight equation for the M8 API to 1800 yards is now: TOF Computed M8 API = (1/((3000/(1800*3))-((0.00372*1)/(2*0.439)*Sqrt(3000)))) TOF Computed M8 API = 3.091277324 Seconds The computed TOF to 1800 yards is 3.09127 seconds. The TOF for M8 API using the NDRC equation is 3.09 seconds. In the real ballistic table the TOF to 1800 yards is 3.08 seconds. The computed TOF is 0.01 seconds longer. A difference of +0.0032%. The high level of accuracy of the NDRC method means that it can be relied upon to compute the TOF M20 APIT to 1800 yards. Based upon the accuracy of NDRC method I’ve set the tracer off time of the M20 APIT to 3.1 seconds. Dispersion Data: The variable DCS uses to describe the weapon dispersion is Da0. In the Western technical literature this variable is equivalent to Deflection Error Probable or Range Error Probable. Error Probable is equal to 0.6745 * the standard deviation of dispersion from the aim point in the x or y axis alone. https://apps.dtic.mil/sti/tr/pdf/AD1009077.pdf Error Probable as a measure of accuracy is more commonly used in Soviet and Russian sources. The Image in the spoiler Below is from a manual on Soviet Aircraft Ammunition from the 1950’s. The Manual gives the error probable for few Soviet Cold War Era aircraft cannons in meters. On the other hand, Western Sources often depict accuracy as the radius or diameter of a circle and a percentage. For example, the 1945 “Air Force Gunnery Manual 64” states the dispersion of the 50 Caliber Browning is a diameter of 4 mils 75%. https://archive.org/details/air-forces-manual-no.-64-fighter-gunnery-firing-rockets-dive-bombing-1-may-1945/page/67/mode/1up To convert the Western accuracy measurement, a diameter of 4 mil 75%, to the same format as DCS uses (Error Probable) we have to do some math. First, We’re going to use the 4 mil 75% accuracy rating of the 50 Caliber and determine the standard deviation of the dispersion, also known as sigma. After, we have determined sigma. It’s relatively easy to convert sigma to Error Probable, then convert Error probable from mils to radians, which is the format DCS uses for the accuracy rating Da0. The value 4 Mil 75% is a function of a circular bivariate normal distribution. The diameter of a circle containing a given probability is = The standard deviation of the distribution of the dispersion (sigma) * sqrt(-8*ln(1-the probability of the circle). Therefore, the diameter of 75% circle is equal to: Sigma * sqrt(-8*ln(1-0.75) = The Diameter of 75% Circle Which simplifies to: Sigma * 3.33021 = The Diameter of 75% Circle Since the document gives us the diameter of the circle (4 mils). We know that: Sigma * 3.33021 = 4 With some simple algebra, we can now determine sigma. By dividing 4 mils / 3.33021 we get sigma 4/3.33021 = sigma = 1.2011 mils Our computed value of sigma agrees with other values of sigma present in the technical literature. Standard Deviation Source. From “Analytical Studies in Aerial Warfare” https://archive.org/details/analyticalstudie02bush/page/105/mode/1up Now that we have sigma, all we have to do is convert sigma to Error Probable. Which is pretty straight forward. Sigma * 0.6745 = Error Probable (Mils) 1.2011*0.6745 = 0.810 Error Probable (Mils) The variable for dispersion in DCS, Da0, is in radians, To convert mils to radians. Multiply by 0.001 Thus Da0 50 Cal Mod = 0.810 *0.001 Da0 50 Cal Mod = 0.00081. The current value of Da0 for the 50 Cal is = 0.00085, Which equates to a standard deviation of 1.26 Mils. The standard deviation of the 50 Cal Mod is 1.2 mils. The net result of the mod is a 10% reduction in area of Circle Error Probable. In the web based graphing application Desmos. I’ve created a simulation that randomly places some random normally distributed "bullet impacts." While plotting the Circle Error Probable aka the 50% impact circle of dispersion. Link to the Dispersion Sim https://www.desmos.com/calculator/srjak2emph With this tool we can easily create an accurate depiction of the Modded Dispersion, which has a 1.41 Mils 50% radius. Thus the radius of Circle Error Probable for the Mod is 1.41 Mils. And the radius of 50 % percent circle / Circle Error Probable for the default DCS World War 2 50 caliber Projectiles is 1.48 mils. Yeah that was a lot of math for not much of a change in dispersion. The size of the dispersion in DCS before barrel heat effects are applied is only slightly off. However, this small change does make the bullets more historically accurate, which is the intent of this mod. While we did not end up with large change to the dispersion. I did learn a lot from research that went into determining the appropriate value of Da0. I ended up with a much better understanding of how the accuracy values of the weapons in DCS relate to the real world accuracy ratings. This knowledge will end up helping me with a few other projects I have in mind too. With the dispersion taken care of, we have just about covered all the changes this mod makes to the 50 caliber projectiles. However we do have a few miscellaneous changes to cover Other Changes and Final Notes: DCS also has a variable which randomizes the muzzle velocity of the project, Dv0. This is set to 0 in the mod during test and validation and has been left off. The duration of the smoke effect has been reduced. In DCS the Smoke effect of the tracer effect doesn’t match the trajectory of the bullet. The smoke effect just travels straight out from the gun barrel. Thus the smoke tends to hinder aiming. The thickness and amount of smoke produced by the effect also obscures the visual signature of the tracer glow. Which also greatly reduces the effectiveness of the tracer as an aiming aid. Thus the smoke time has been reduced from 0.5 Seconds to 0.1 Seconds. I’ve also changed the projectile type of the M1 Incendiary from Ball to AP. The M1 Incendiary was manufactured around a tubular steel dowel / frame. The thick steel sleeve and high muzzle velocity gave the M1 Incendiary the ability to penetrate armor up to 7/8 inches thick. This excerpt is from the US Army Air Forces Aircraft Evaluation Report of The Messerschmitt -109F Link to the 109F report: https://stephentaylorhistorian.files.wordpress.com/2020/04/bf-109f-evaluation.pdf Given the M1-Inc’s ability to penetrate fairly thick armor, the change in projectile type is reasonable. That covers all the changes this mod makes to DCS 50 caliber projectiles. If you have read this far down I want to thank you for taking the time to do so. If you have any questions please feel free to ask. I’m always happy to help.

I found the source for the DCS pattern. It's from the North American Aviation Version of the flight Manual. https://app.aircorpslibrary.com/document/viewer/fmp51na5914 The pattern. The DCS pattern is an almost exact fit of this pattern. The NAA manual pattern being the dashed lines. https://www.desmos.com/calculator/2dnjxa31ca It does look like someone from NAA may have miss interpreted the Air Force pattern. As the NAA pattern also mirrors the dispersion pattern. https://www.desmos.com/calculator/ngk08zcyuh And the NAA pattern Disappears from all the documents published after this manual. NAA Harmonization / Convergence Pattern K-14 Sight NAA Manual Azimuth Azimuth Degrees Elevation Elevation Degrees Gun 1 72.5 38.375 0.006623 0.3794699477 0.006348 0.3637136083 Gun 2 82.08823529 36 0.005002764706 0.2866373035 0.007493 0.4293172759 Gun 3 89.125 39 0.005951 0.3409671839 0.005002 0.2865934891

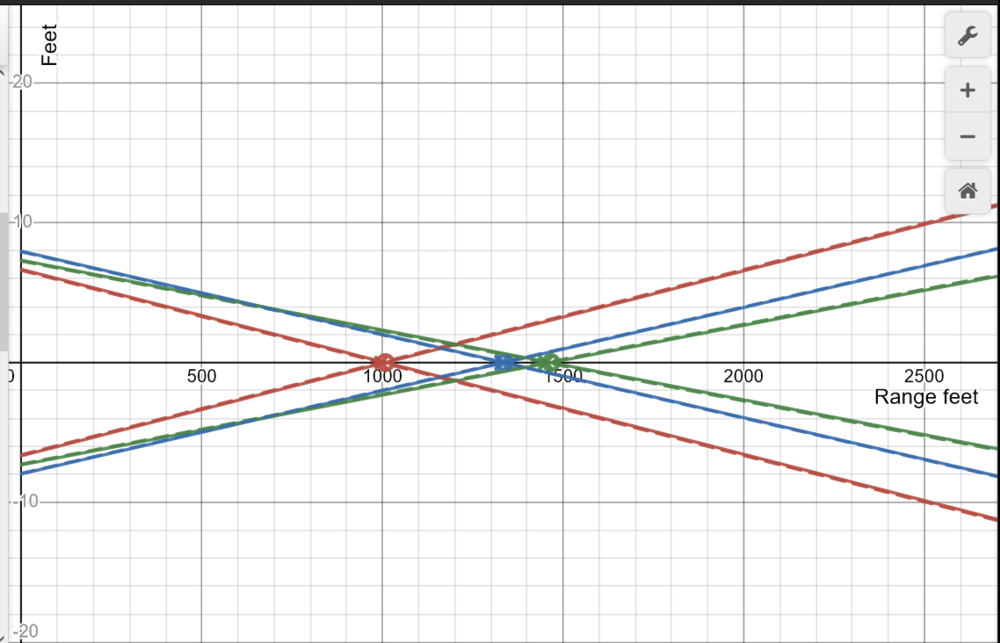
I know of two other official harmonization / convergence patterns for the P-51 D. The DCS P-51 does not match either of these. The two other harmonization / convergence patterns I know of, come from the P-51 maintenance manual. In the manual there is a 300 Yard and 250 Yard Harmonization / Convergence pattern. https://stephentaylorhistorian.files.wordpress.com/2020/04/p-51d-part-2.pdf I’ve plotted both patterns in Desmos so we can compare them to the DCS. Links to the graphs are provided as well 300 Yard Harmonization / Convergence at 0 mph https://www.desmos.com/calculator/hp4q0ry43j 300 Yard Harmonization / Convergence at 300 mph https://www.desmos.com/calculator/ygsuwf5tge Below is a table with the 300 yard 1000 inch boresight target data, gun azimuth and elevation settings. 300 Yard 1000 inch Card Horizontal Distance V Distance Azimuth Azimuth Degrees Elevation Degress Gun 1 70.25 38.125 0.008873 0.5083854516 0.006598 0.3780375532 Gun 2 77.5 37.5 0.009591 0.5495238213 0.005993 0.3433736066 Gun 3 83.375 37.125 0.011701 0.6704179161 0.006877 0.3940230757 The 250 Yard Harmonization / Convergence Pattern at 0 mph https://www.desmos.com/calculator/qkmq0qv6gi The 250 Yard Harmonization / Convergence Pattern at 300 mph. https://www.desmos.com/calculator/nfqmso8h1m Table for the 250 yard Harmonization / Converge settings. 250 Yard 1000 inch Card Horizontal Distance V Distance Azimuth Azimuth Degrees Elevation Elevation Degrees Gun 1 68.875 38.125 0.010248 0.5871671485 0.006598 0.3780375532 Gun 2 79.5 37.5 0.007591 0.4349322623 0.005993 0.3433736066 Gun 3 82.25 37.125 0.012826 0.734875668 0.006877 0.3940230757 DCS Harmonization / Convergence at 0 mph https://www.desmos.com/calculator/3ywwxznhdb DCS Harmonization / Convergence at 300 mph. https://www.desmos.com/calculator/yvfsqh0yim The current DCS P-51 harmonization pattern seems to be configured to match the depiction of the 75% 4 mil dispersion of the 50 cal. In the graphing program we can compute the and plot the 4 mil dispersion zone. https://www.desmos.com/calculator/wlsqlyaxtj Note that the convergence pattern of the DCS P-51 matches the plot of the dispersion zones almost perfectly. Maybe someone changed the azimuth to match the dispersion zone? However the current configuration of the DCS harmonization pattern does not seem to match anything I can find. Following the instructions in the Harmonization manual, we can create a 1000 inch boresight card for the DCS P-51 Harmonization / Convergence settings. Presenting the data in a table. DCS P-51 Harmonization H Distance V Distance Azimuth Azimuth Degrees Elevation Elevation Degrees Gun 1 72.50820213 38.37000152 0.006615 0.379 0.006352998477 0.364 Gun 2 82.09935834 35.49939203 0.004992 0.286 0.007993607974 0.458 Gun 3 89.12442725 39.51650382 0.005952 0.341 0.004485496178 0.257

null The azimuth Angle on the P-51 guns seems off a bit. Per this post https://forum.dcs.world/topic/79688-convergance-and-gun-options/page/2/#comment-1725050 The expected convergence pattern should mirror the one in Air Forces Manual No. 64 Fighter Gunnery https://archive.org/details/air-forces-manual-no.-64-fighter-gunnery-firing-rockets-dive-bombing-1-may-1945/page/110/mode/1up Which is the pattern as depicted in the manual Fighter Gun Harmonization. https://archive.org/details/aaf-manual-200-1-fighter-gun-harmonization/page/37/mode/1up From the DCS P-51 lua file we have the azimuth for the all 6 of the guns. DCS Gun 3, Outboard: gun azimuth_initial = 0.341, DCS Gun 2, Middle Gun: gun azimuth_initial =0.286 DCS Gun 1, Interior Gun: azimuth_initial = 0.379, The unit is likely degrees. Converting to radians gives us. DCS Gun 3, Outboard: gun azimuth_initial = 0.005951, DCS Gun 2, Middle Gun: gun azimuth_initial =0.004991 DCS Gun 1, Interior Gun: azimuth_initial = 0.0066147, The position of the gun is also given in meters within the lua file. With this data we can compute at which range the guns will converge. Using the graphing application Desmos, we can overlay the and compare the harmonization pattern of the DCS P-51 to the one depicted within the manual. We’ll straighten this up a bit and import it into Desmos and scale it. Link to the Desmos Convergence Calculator. https://www.desmos.com/calculator/ujiueojjjp Using azimuth angles and gun positions from the lua file. We plot the convergence pattern of the DCS P-51 at 0 mph. Note that interior guns, Gun 1, the red lines, Converge At 1007. Feet The middle Guns, Gun 2 ,the green line, converge at 1466 feet The exterior guns, Gun 3, the blue line, converge at 1337 feet. Let’s remove the graphic for a clear look at the DCS pattern. It’s important to note that the Harmonization Pattern and settings depicted in the manual are configured for an airspeed of 300 mph. At 300 mph in the real P-51 The Interior Guns, Gun 1, Converge at 1000 feet The Middle Guns, Gun 2, Converge at 1100 feet The Exterior Guns Gun 3, Converge ar 1200 feet. Removing the Graphic for a clear view. However the azimuth of the guns is actually set to a larger angle than is depicted. This is because the forward velocity of the aircraft alters the velocity vector of the projectile. This reduces the effective azimuth angle of the trajectory. The change in the effective azimuth angle can easily be calculated; The Fighter Gun Harmonization Manual and AAF Manual 335-25 both provide the relevant equation. Which I will call the trajectory correction function. The Manual Fighter Gun Harmonization https://archive.org/details/aaf-manual-200-1-fighter-gun-harmonization/page/7/mode/1up And AAF Manual 335-25 https://books.google.com/books/content?id=81krAQAAMAAJ&pg=PA331&img=1&zoom=3&hl=en&bul=1&sig=ACfU3U1BRdZA_vO5KY8Ylk_Y-i3WWQQ4mQ&ci=4%2C1%2C993%2C1326&edge=0 The trajectory correction function is ((Vias in FPS) * the basic azimuth angle of the gun) / the muzzle velocity of the gun. If we apply this correction factor to the DCS P-51 guns at 300 mph, the harmonization pattern moves well beyond what is depicted in the manuals. The Interior Guns, Gun 1 Converges at 1200 feet at 300 mph. The Middle Guns, Gun 2, Converges at 1751 feet at 300 mph The Exterior Guns, Gun 3, Converges at 1598 feet at 300 mph A more clear view with the graphic removed. The basic Azimuth angle for the real P-51 can easily be computed with the information provided in the Harmonization manuals. All we need is the position of the guns and the data from the 1000 inch boresight target. The basic azimuth angle of the gun is (Horizontal position of the Gun from the Center line - The position of the gun on the 1000 inch boresight card) / (range to the card 1000 inches). This gives the basic azimuth angle of the gun. For Gun 1 the equation is ( 79.123-71.25)/ 1000 = 0.007873 Which is the basic azimuth angle for the Gun 1. Lets Create a virtual boresight target in graph and plot the trajectory / basic angle of the guns. The line of sight of the guns does pass through the boresight target, however the convergence pattern of the gun is short of the chart. If we fired the guns at 0 mph with this pattern. Gun 1 Interior would Converge at 837 feet. Gun 2 Middle would Converge at 925 feet Gun 3 Exterior would Converge at 1012 feet. Let compute the trajectory correction for Gun 1 at 300 mph and plot the convergence pattern again. The Trajectory correction for Gun 1 is. ((Vias in FPS) * the basic azimuth angle of the gun) / the muzzle velocity of the gun. ((300 mph *1.467) * (0.007873)) / 2700 = .001283299. We then subtract the trajectory correction factor from our computation of the azimuth angle of the gun. Lets compute the effective azimuth angle of Gun at 300 mph (( 79.123-71.25)/ 1000)- 0.001283299. = .006589701= The effective azimuth angle of Gun 1 at 300 MPH Lets plot the effective line of sight of gun 1 with the trajectory correction for 300 mph With the trajectory correction Gun 1 matches the harmonization pattern as depicted in the manual. And Converges at ~ 1000 feet. Let's do the same for the other guns now. And without the graphic for clarity. All we have done is use the data and equations from the manuals, and computed the trajectory. The basic azimuth angle will always be greater than the effective azimuth angle, if the convergence pattern is configured for an airspeed greater than 0. In the P-51 maintenance manual there are settings for a 300 yard and 250 yard convergence pattern. This patterns are also based on a air speed of 300 mph. Above we depict the basic azimuth with a sold line and the effective azimuth angle at 300 mph with the dashed line. Note that the effective azimuth angle with trajectory correction converges at 300 yards, where it should. While the basic azimuth angle passes through the center of the boresight target, but converges well short of 300 yards. Therefore the azimuth angle for the guns should be set to basic azimuth angle as computed from the 1000 inch boresight target.

I realize the formatting of some of the tables is not ideal. If you wish to read this document in google docs, a link is provided below. The tables can also be viewed from within the spreadsheet. Link to the google doc version of this post. https://docs.google.com/document/d/1LCRhctj31-tdp9ehzIFUILtF0OhItK6ROC2AhEopWXA/edit?usp=sharing Link to spreadsheet. https://docs.google.com/spreadsheets/d/1h3fCvpvdc7j2f3iyASP3ft4ogz3koOjQksYY3i7Bjd8/edit?usp=sharing Ballistic Tables and Ballistic Calculators Firing Tables for many of the bullets used in the war is particularly difficult to find. Especially for aircraft weapons. The aircraft version of the 50 caliber Browning has a 36 inch barrel. Thus has slightly reduced muzzle velocity when compared to the Heavy barrel version of the gun used in ground applications. Therefore, what data is available, for the various 50 caliber ammunition, may not be applicable to an aircraft machine gun. However we can recreate the firing / ballistic tables for various bullets by using the methods and equations from the world war 2 era.. The ballistic tables of this era were computed based on ballistic coefficients and a few different methods of integrating through the appropriate ballistic table. This process is often called the Siacci Method of integration. US military manuals and academic papers of this era indicate the use of Siacci Tables integration methods was the standard process of computing ballistic and firing tables. See The spoiler for examples. The ballistic performance data of the bullets from the World War 2 era is written in terms of a ballistic coefficient. Through the use methods and mathematics of this era, it is possible to create and recreate accurate ballistic and firing tables for the various 50 caliber bullets. Even if the data is lost or missing from the historical record. First, it’s helpful to define the meaning of the term ballistic coefficient. The ballistic coefficient of this era is a way of relating the drag of the bullet in question to an idealized version of a bullet of similar shape. Therefore the ballistic coefficient consists of two variables, a type and a factor. For example in the BRL report. “Ballistic Coefficients of Small Arms Bullets Of Current Production” https://apps.dtic.mil/sti/pdfs/AD0491936.pdf All of the 50 caliber bullets have a type of C5 / G5. While the factor varies 0.414 for the M1 Incendiary to 0.460 for the M2 Ball. We would say the Ballistic Coefficient of the M1 incendiary is C5 / G5 0.414. The projectile type is as important as the factor. As the bullet is matched to a projectile type with a similar drag coefficient. The Equation for the ballistic coefficient as given by Mc Coy is Cj = (mass (lbs)/ form factor (i_j) * diameter (inches)^2) Where j is is of projectile type and the form factor, i, = (CD of projectile) / ( CD of the projectile type.. Ie G5, G6, ect) https://archive.org/details/ModernExteriorBallisticsTheLaunchAndFlightDynamicsOfSymmetricProjectiles2ndEd.R.McCoy/page/n98/mode/1up If we take the weight and form factor data for the M1 incendiary from “Aerodynamic Data for Spinning Projectiles. We can compute the ballistic coefficient of this bullet. Projectile Name: Projectile Weight Grains Projectile Diameter Projectile Type Form Factor M1 Incendiary 625 0.5 5 .86 The first step is to convert the projectile weight from Grains to lbs. We do this by dividing the weight by 7000, which gives us 0.08928 lbs. The ballistic coefficient is then computed as 0.08928 / (.86 * 0.5^2) = 0.41525 Thus the ballistic coefficient of the M1 Incendiary is C5 / G5 0.41525. The test of the production gave a BC of .414 to this same bullet. The ballistic coefficient and form factor are determined either through firing tests or in from a wind tunnel test. The drag of the projectile is then matched to the appropriate projectile type and the ballistic coefficient is determined. The standard Projectile types are G/C 1 through 8. Drag profiles in the for KD are given Hitchcock's work Aerodynamic Data for Spinning Projectiles. https://apps.dtic.mil/sti/pdfs/AD0800469.pdf Pics of both in the spoiler below Data from the BRL on the ballistic coefficients and form factors of a variety of projectiles is readily available. Most of the data is from the World War Two era also. Two of the best sources for this type of data are the reports “Aerodynamic Data for Spinning Projectiles” and “Form Factors of Projectiles”. Excerpts and links to both reports are contained in the spoiler below along with a few other sources. We will use this data to create a ballistic table similar to the ones in the Air Force Manuals of the era. https://www.google.com/books/edition/AF_Manual/81krAQAAMAAJ?hl=en&gbpv=1 We’ll use two methods to create our tables. The full long form of Siacci Method for Flat Fire Trajectories as described by McCoy, Hitchcock and Kent, and a simpler method that was developed specifically by the BRL to produce firing tables for aircraft weapons. The methodology for the Siacci method is described in detail with examples. In Modern Exterior Ballistics https://archive.org/details/ModernExteriorBallisticsTheLaunchAndFlightDynamicsOfSymmetricProjectiles2ndEd.R.McCoy/page/n97/mode/2up?view=theater This method involves looking up data in a table of figures for our bullet type. Then modifying these values based on the ballistic coefficient of the bullet. For example, In the report “Form Factors of Projectiles”. The BRL gives the 50 Caliber M1 Incendiary A ballistic Coefficient of C/G 6 .387. If we assume a muzzle Velocity of 2990 our Siacci operations look a bit like this. By interpolating through the G6 Siacci Table and applying the appropriate equations we are able to compute the bullet drop, the time of flight, and the impact velocity of the bullet at any range. In order to determine the accuracy of this method, Let’s compare a Siacci Calculation for 50 cal AP M2 to the ballistic table in Air Force Manual AFM 335-25 Fighter Weapons. We’ll compare the time of flight and vertical deflection in inches, which is also known as the bullet drop. At sea level with a true air speed of 0 mph. For our Siacci Calculations we’ll set the muzzle velocity to match the chart, 2700 fps, and use the a Ballistic coefficient of C5 / G5 0.458. As this matches the BRL data for a world war 2 version of the M2 AP. In the spoiler below we have the Air Force Firing Table for the 50 Caliber M2 AP. https://www.google.com/books/edition/AF_Manual/81krAQAAMAAJ?hl=en&gbpv=1 I’ve added the Air Force firing table for the 50 Caliber M2 AP to a spreadsheet in order to compare it to the results of the Siacci method of calculating firing tables. Below is the Air Force Firing Table for the 50 cal AP M2 in table form from the spreadsheet. Note that gaps in data reflect those in the actual firing table. In the spoiler below we have A Similar Table with Values computed with the Siacci method. We can also compare the Time of Flight Vs Range of the Air Force Table and the Siacci Method. As this will also give us a sense of the drag coefficient of both bullets. The results of the Siacci table are very similar to the Air Force Firing Tables. The average difference in time of flight between the two firing tables is 0.007 second. Some of the difference being a function of the original tables using a limited number of decimal places. The slight difference between the two data sets, indicates the Siacci Method, when using the appropriate tables, can produce results which effectively match the tables in the primary sources. Thus providing us with a valid means to create ballistic tables for projectiles where no such data exists. While the Siacci method is accurate and flexible. The manual calculations of firing tables using the Siacci method was still very time consuming. During the war the demand for firing tables was at an all time high. Therefore the BRL and the National Defense Research Council (NDRC) developed a faster method to calculate firing tables. The application being primarily limited to aircraft weapons. The method is described in the Report, “NDRC Analytical Studies In Aerial Warfare: “Pages 28 to 30. https://www.loc.gov/resource/gdcmassbookdig.analyticalstudie02bush/?sp=28 The NDRC report provides two derivations of a time flight equation and one equation which computes the vertical deflection / drop of bullet (Q) as function of Time of Flight (t) The short version of the time of flight equation is tof= (range / sqrt v0)/((sqrt(v0)-(((.00186*rho)/bc)*range And the longer version of this equation is tof= (1/((V0/Range)-((k_star*rho)/(2*BC)*Sqrt(v0)) Where k_star = 0.00372 for feet per second Both TOF functions return the same value given the same input. The second version is a bit more flexible as the constant k star can be altered based on the desired unit of measure. The equation for the bullet drop at a given range is given as: Vertical Deflection Feet: Drop = .5*g*t^2*(1-((rho *.00372)/(3*BC))*(Range/(sqrt(V0))) Where v0 = the muzzle velocity + the aircraft velocity in fps Range is the down range distance to the target in feet. Rho is the relative Ballistic Air Density And bc is the C5 ballistic coefficient of the projectile. Thus we come to the major limitation of this equation. It is valid for projectiles with a C5 / G5 ballistic coefficient. Which may not always be the best drag function for a projectile. We’ll circle back to this in the end. For now, let's just compare these equations to the Air Force ballistic / firing table For the 50 Cal AP M2. In the spoiler below is a ballistic / firing table computed using the NDRC method. It is in the same format as the Air Force Firing Table. In the spoiler below is a graph comparing the bullet drop Vs range, aka the trajectory, of the Air Force Table and the trajectory of the bullet we computed via the NDRC method. Along with the time of Vs Range. The NDRC Method actually matches the Air Force Ballistic Table more closely then the Siacci Method. The average difference in time of flight between the NDRC method and Air Force Firing Table is only 0.0052 seconds. The NDRC method also provides an accurate means of computing firing tables. Which shouldn’t be a surprise as according to the NDRC study many of the aircraft ballistic tables of the era were generated with this method. Let's look at one more case. The Aircraft is moving at 300 mph TAS, the density ratio is .6, which corresponds to an altitude of about 15,0000 feet. This altitude was chosen because the density ratio of both the Ballistic and NACA atmospheric models are about the same and it's the altitude for which all the convergence patterns are configured too. In the spoiler We Have the firing table from the Air Force Firing Table and a set of values computed with the NDRC method. In the spoiler below there is a graph comparing the Bullet Drop (Trajectory) and time of flight of the NDRC Method to the Air Force Firing table under the same conditions. On average ,the NDRC method’s time of flight is within .0038 seconds of the chart. Even under flight conditions at altitude, the NDRC method can accurately reproduce the Air Force Firing Tables. Using the Siacci Method we can also compute the trajectory and time of flight under the same conditions. Density Alt .6, TAS 300 MPH. If we overlay all 3 data sets. The results are nearly identical. The marginal differences from the NDRC method, Siacci method and the Air Force Table. May also be the result of some other ways error may have been introduced into the Air Force firing table. These sources of discrepancy may be a result of the earlier version of M2 AP having a higher ballistic coefficient then bullets produced after 1943. If we recompute the ballistic table using the NDRC method and change the BC to .471, to match BRL data for the pre 1943 version of the M2 AP. The average difference in TOF between the NDRC ballistic table and the Air Force firing table. Is the lowest of all the computations presented thus far at 0.002447 second. The same is true for the calculations of the bullet drop. Using a BC of 0.471, the average difference between the NDRC method and the chart is 0.373 inches. These results seem to indicate that the Air Force Ballistic Table for the M2 AP may have been computed for a heavier version of the M2 AP with a slightly higher (better) ballistic coefficient than the production bullets. There may also be some discrepancy between the results due to the fact that a graphic method of interpolation was used in parts of the original Air Force Firing Table. There are also reports from BRL which indicate that the Aberdeen Proving Grounds was having troubles with their measuring equipment .The equipment error caused the institution to issue lower ballistic coefficients to projectiles prior to August 1’st of 1944. Given that the Air Force Firing Table is based on Aberdeen data from prior to August 1’st it’s possible Both the NDRC and Siacci method show good agreement with the Air Force firing tables across a range of circumstances. Therefore, utilizing either the NRDC method with the appropriate ballistic coefficients from period data is a valid way to generate the type of ballistic data needed to implement any of the 50 caliber bullets within DCS. Below is a link to my spreadsheet where I have performed these computations. Most of the work haiving been performed in the Ballistic Calculator tab. Most of the functions and computations should be readable. The idea being that anyone can take a look at the math behind these calculations. There is also a page containing various images and links to the source data. Much of the document however is a work in progress. While parts of the spreadsheet can be useful, it may not be particularly user friendly. It’s easy to mess up a computation. https://docs.google.com/spreadsheets/d/1h3fCvpvdc7j2f3iyASP3ft4ogz3koOjQksYY3i7Bjd8/edit?usp=sharing Thanks for reading this far. I hope this exercise has been insightful as it has been for me. Below are some additional thoughts on the accuracy of these methods. It got a bit longer than I would have hoped, but if you’re interested in this kind of thing you may find it worth reading. As final thought I want to discuss some limitations of approaches presented in this post. While the NDRC function is very useful there are some very real limitations to it. The model is based on the 3/2 drag power law. Meaning below half the muzzle velocity the data becomes unreliable. However there are also very useful ways to use the data generated from the NDRC tables. For example the impact velocity can be computed through a derivation of the 3/2 drag law. Impact Velocity = (Range^2) / (TOF^2) * V0 Which can provide for a more accurate basis of drag coefficient computation. The same information can also be obtained from the Siacci Methods however the process is more tedious. Both the NDRC and Siacci methods may also not be as accurate as more modern numerical techniques. Both methods depend on how well the projectile matches the drag coefficient of its associated type. The war time paper “Ballistic Coefficients of Small Arms Bullets Of Current Production” https://apps.dtic.mil/sti/pdfs/AD0491936.pdf Assigned almost every projectile a C5 / G5 ballistic coefficient. A few years after the war, the projectile types and form factors of some of the more common 50 caliber bullets changed. The M1 incendiary goes from a G5 0.414 in 1944 to a G6 0.387 in 1951. If we compute the impact velocity for both bullets with the Siacci method, On average the G6 0.0387 version impacts 35 to 45 fps faster than the G5 0.414 Ballistic coefficient. Which indicates that the BRL thought the C5 / G5 ballistic coefficient resulted in to much drag. In the spoiler below is chart comparing the impact Velocity Vs Range of the M1 incendiary with both ballistic coefficients. The story is similar for the M8 API, which is considered one of the most effective 50 caliber bullets. During the course of the War the bullet was given 3 different G5 ballistic coefficients. None of the G5 ballistic coefficients were accurate enough as there was considerable variation in the form factor as function of mach. Thus a custom drag function / bullet type was created for the M8 API. Image of custom drag function and conversion to modern CD notation in spoiler A set of Siacci tables was created for the M8 drag function. There A 1996 report by the BRL indicates that the CDO of the M8 drag function is 4% lower in the supersonic regime. However examining data in detail also raises some questions. Plotting the old drag function on top of the 1996 data, shows that the old drag function actually has a higher supersonic drag coefficient than the author says. It is possible to match the data by reducing the old drag profile by 4% though. Given total drag on the projectile is a function of the CD0, the quadratic yaw drag coefficient and the angle of attack of the bullet. McCoy’s plot of CDO does not represent the total drag coefficient of the bullet in flight. The older drag function however computes the drag as a function of trajectory angle. Which may provide a more accurate assessment of the total drag on the M8 API during flight condtions. A comparison of both methods would require a full 6 dof simulation with McCoy’s data and a similar calculation using the Siacci Tables for the M8. However both sets of data would need to be checked against some type of test data. The best set of data publicly available are either the Air Force Firing tables, or the 1946 copy of the M8 firing table for the heavy barrel machine gun. Which puts us back to square 1. This has led to some reluctance on my part to take the time to implement M8 Siacci Tables into my spreadsheet. It’s a lot of data entry and I’ve already spent way too much time on this. The World 2 Data G5 data is probably accurate enough for the purpose of video games.

Muzzle Velocity Part 2: More Data. There is also some secondary data on muzzle velocity that also agrees with the numbers provided in my first post. We’ll consider some indirect evidence, particularly what is known as Instrument Velocity. Along with the methods that were used within the War and post war era to compute muzzle velocity. In many of the source documents bullet velocity values are given at a specific distance. From the Small Arms Development Report for example. The velocity of the M2 AP from a 36 inch barrel at 78 feet is 2810 +- 30 fps. https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13268 The Ballistic Research Laboratory (BRL) calls the bullet velocity at 78 feet, the instrument velocity. Ballistic Coefficients of Small Arms in Production 1944 https://apps.dtic.mil/sti/pdfs/AD0491936.pdf The standard setup used by the BRL was to place the first chronograph 28 feet from the barrel, and the second 128 feet from the barrel. Thus the distance from the midpoint of the chronographs was 78 feet and the chronographs were 100 feet apart. This paper also gives us 2 equations to compute the muzzle velocity from the instrument velocity. Muzzle Velocity V0^.5 = v^.5 + (.059 rho/C5 Ballistic Coefficient)*Distance(78* 0.5) We can simplify this a bit and just get the muzzle velocity by squaring the right side of the equation. Muzzle Velocity = (Instrument Velocity ^.5 +((.059 * 0.07513/ Ballistic Coefficient) * ( 78 *05))^2. Note, that rho is the ballistic sea level air density in lbs per foot^2. The report also gives us this equation. The muzzle velocity - the instrument velocity = 4.3* (78^2/1000) Mathematically this formula tells us to add about 26 fps to the instrument velocity. For example the instrument velocity of the .50 caliber M2 AP is given as 2810 fps. The muzzle velocity is 2836 fps. Which is the figure quoted in many of the post 1944 reports. Such as the 1945 version of manual “Terminal Ballistics Data”. https://cgsc.contentdm.oclc.org/digital/collection/p4013coll8/id/2373/rec/8 There is yet another way we can compute the muzzle velocity from instrument velocity. Since we have the ballistic coefficients of these bullets it’s possible to work backwards through the Siacci tables and compute the muzzle velocity. I’ll spare you the details of integration of the Siacci tables. However the approach is validated within Ballistic Coefficients of Small Arms in Production 1944, and by McCoy in Modern Exterior Ballistics. https://apps.dtic.mil/sti/pdfs/AD0491936.pdf So let's apply our 3 equations to compute the muzzle velocity from the Instrument Velocity. Then will compare the results to the values given in th 19. Well use ballistic coefficients given in 1944 report, The Instrument velocities from the Ordendance Department’s Small Arms Development Report and the post war report Form Factor of Projectiles BRL Report 564 1951. Value: M2 AP API M8 M1 Incendiary BC C5 0.458 0.439 0.414 Instrument Velocity at 78 Feet 2810 2910 2950 Instrument Velocity At 78 Feet: mps 856.446 886.925 899.116 Muzzle Velocity BRL C5 Method 2850.160 2952.641 2995.534 Instrument Velocity + 26 fps 2836 2946 2976 Muzzle Velocity Siacci 2843.341 2945.325 2987.641 Muzzle Velocity 50 Cal Manual 1946 2840 2950 2990 All three methods used to compute the muzzle velocity from the instrument velocity show good agreement with the muzzle velocity cited in various source materials. This all just amounts to another piece of evidence indicating that muzzle velocities for the 50 calibers in game are a bit too low. Data Sources and links in the spoiler

I’ve been reviewing a lot of the historical data on the various 50 caliber bullets used in World War 2. The DCS values for muzzle velocity and weight are different from data in the historical and contemporary sources in some instances. In the first part of this post I will present data showing the muzzle velocities, weight and dispersion for these bullets. All the data presented will be for the 36 inch Barrel Aircraft Machine Gun version of the Browning 50 caliber. In the second part, we’ll get a little more in depth with data. We will also construct firing tables and compute the trajectories of the bullets using historical methods and data. With that out of the way. Let's begin by comparing the DCS data in the CoreMods\WWII Units\Weapons\Weapons.lua file to some contemporary and historical data. The table Below shows the values In game Vs the historical data. I’ve also added some data for the M1 incendiary bullet, which was one of the most commonly used in American aircraft. DCS M2 AP DCS M8 API DCS M20 APIT M2 AP Historical Data M8 API Historical Data M20 API Historical Data M1 Incendiary V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) V0 (Muzzle Velocity MPS) 830 860 875 864 899 899 912 Bullet Weight Kg Bullet Weight Kg Bullet Weight Kg Bullet Weight Kg Bullet Weight Kg Bullet Weight Kg Bullet Weight Kg 0.0458 .0403 0.0410 0.046 .042 .0396 0.040049 Da0 (Dispersion) Da0 (Dispersion) Da0 (Dispersion) Da0 (Dispersion) Da0 (Dispersion) Da0 (Dispersion) Da0 (Dispersion) 0.00085 0.00085 0.00085 0.001 0.001 0.001 0.001 100% Dispersion: Mils 100% Dispersion: Mils 100% Dispersion: Mils 100% Dispersion Mils 100% Dispersion: Mils 100% Dispersion: Mils 100% Dispersion: Mils 6.8 6.8 6.8 8 8 8 8 Below is a table of muzzle velocities for the .50 Caliber M2 AP, M8 API and M1 Incendiary in the various historical and contemporary documents.The table also includes a link to the source material. Bullet: Muzzle Velocity: FPS Muzzle Velocity MPS: Source: Link To Source M2 AP 2835 864.07 Terminal Ballistic Data 1945 https://cgsc.contentdm.oclc.org/digital/collection/p4013coll8/id/2373/rec/8 M2 AP 2845 867.11 Terminal Ballistic Data 1944 /43 https://cgsc.contentdm.oclc.org/digital/collection/p4013coll8/id/2327/rec/1 M2 AP 2845 867.11 Test Method Standard V50 Ballistic Test For Armor MIL STD-662F 1997 https://www.abbottaerospace.com/downloads/mil-std-662f-v50-ballistic-test-for-armor/ M2 AP 2845 867.11 NDRC Study Effects Of Weapon Impacts https://www.loc.gov/resource/gdcmassbookdig.effectsofimpacte01unit/?sp=421 M2 AP 2840 865.59 TM 9-225 Browning Machine Gun .50 Caliber AN-M2 Aircraft https://www.google.com/books/edition/Browning_Machine_Gun_Caliber_50_AN_M2_Ai/nXySRue3QAYC?hl=en&gbpv=1 M2 AP 2845 867.11 TM-9-2200 Small Arms https://archive.org/details/TM9-2200/page/n203/mode/2up M2 AP 2840 865.59 TM 9-219 AN M3 Basic Aircraft Machine Gun https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=7268 M8 API & M20 APIT 2946 897.89 AFM 51-44 Fighter and Fighter Bombers Employment in Tactical Air Operations https://archive.org/details/fighter-fighter-bomber-employment-in-tactical-air-operations-usaf/page/55/mode/1up M8 API & M20 APIT 2950 899.12 TM 9-225 Browning Machine Gun .50 Caliber AN-M2 Aircraft https://www.google.com/books/edition/Browning_Machine_Gun_Caliber_50_AN_M2_Ai/nXySRue3QAYC?hl=en&gbpv=1 M8 API & M20 APIT 2950 899.12 TM 9-219 AN M3 Basic Aircraft Machine Gun https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=7268 M8 API (45 Inch Barrel) 3045 982.07 FT 0.50AA-T1 1946 Firing Table M8API Heavy Barrel https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=3561 M1 Incendiary 3100 944.83 TM-9-2200 Small Arms https://archive.org/details/TM9-2200/page/n203/mode/2up M1 Incendiary 2990 911.31 TM 9-225 Browning Machine Gun .50 Caliber AN-M2 Aircraft https://www.google.com/books/edition/Browning_Machine_Gun_Caliber_50_AN_M2_Ai/nXySRue3QAYC?hl=en&gbpv=1 M1 Incendiary 2990 911.31 TM 9-219 AN M3 Basic Aircraft Machine Gun https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=7268 Below are images from the sources On Muzzle Velocity. Images Projectile Weight: For the weight data we’ll use one source, the blueprints for the projectiles. The blueprints for the projectiles have two different weights. The Standard weight and the Alternate weight. We’ll be using the Alternate weight of the projectiles, where applicable, the M2 AP, M8 API and M20 APIT. The reason for this is explained below the table. M2 AP 50 M8 API M20 API M1 Incendiary Weight 708 649 620 633 Alternate Core 708 649 612 643.5 std Core 718 662 624 633 Alt Core Kg 0.04588 0.0420 0.0396 DCS KG 0.0458 0.0403 0.041 DCS Grains 706.694 621.829 632.63 M2 AP https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13268 M8 API https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13265 M20 APIT M1 Incendiary According to a Ballistic Research Laboratory Report and Ordnance Research and Development .In 1943, due to supply shortages. The material for all the armor piercing cores was changed in the 50 caliber bullet. This reduced the weight of all the 50 caliber projectiles which made use of an armor piercing core, the M2 AP M8 API, and M20 APIT. The majority of these bullets were assembled with the alternate core. Which is why the weights presented are based on the alternate weight of the projectile. Army Ordnance Research and Development Report Dispersion: Preface, Units of Measure. In the discussion below the data is given in the value of mils. In this case we are referring to milliradians. Where one mil is = 0.057296 degrees. At a range of 100 feet, 1 mil = 1.2 inches. A table from the Air Force Manual Fighter Gun Harmonization provides further detail in the spoiler. According to this comment by Yo-Yo https://forum.dcs.world/topic/207864-closed-m61-dispersion/page/2/#comment-3916757 The 100% dispersion, in mils, of the weapons in DCS can be computed by multiplying the value Da0 by 8000. As 0.0022 * 8 = 0.0176 radians * 1000 = 17.6 mils. Thus we can determine the game value of dispersion , Da0, of a weapon system by dividing the 100% dispersion in mils of the weapon system by 8000. In multiple documents over a period of several years. The Air Force quoted the 100% dispersion circle as 8 mills for the 50 caliber machine gun across multiple aircraft. Another value commonly used throughout the documents is the value for 75% dispersion, which is 4 mils. The dispersion rating of 8 mils 100% is the same as 4 mils 75%. Both ratings have the same standard deviation and are products of the same normal distribution. The dispersion notation of a percentage and value in mils is based around normal distribution. The equation used to compute the value is given in the National Defense Research Committee (NDRC) report Analytic Studies in Aerial War. https://www.loc.gov/resource/gdcmassbookdig.analyticalstudie02bush/?sp=38 Equation 11 states: The diameter of the dispersion in mils is = the standard deviation of the distribution * the square root of 8* ln (100/(100- The percent value of the circle) The equation uses whole numbers as the input to compute the diameter of the dispersion. For, example the 75% circle, where sigma is the standard deviation of the dispersion and is = 1.2 mils. The equation is (1.2*(sqrt(8*ln(100/(100-75))) = Diameter 3.996 mils By setting sigma to 1.2 and using the equation to compute we get a result that approximately matches the data in the historical sources. Diameter mils Sigma mils % circle 3.996262134 1.2 75 8.071276938 1.2 99.65 Having established a standard deviation for the distribution. We can now compare our results to some of the historical data. Below I will present the historical sources and links. As a side note it looks like there may have been a typing error when the dispersion was computed. If we work backwards from the DCS dispersion value and compute the standard deviation of the dispersion, in game. It looks like someone may hit 1.02 instead of 1.2 when they computed the value of Da0. Da0*8000 = 100% mils The DCS value for the 100% dispersion in mils = .00085. Thus Da0 *8000 = 6.8 mils 100%. If we use the NDRC dispersion equation to find the 99.65% radius the standard deviation is 1.02. As (1.02*(sqrt(8*ln(100/(100-99.65))= 6.86 Da0 All DCS 50 Cals Dao * 8000 =mils 100% DCS 50 Cal Std Dev(Sigma) DCS 100%Radius NDRC Method 0.00085 6.8 1.02 6.8605 On to the sources and pics The Standard Deviation (sigma) of 1.2 mils agrees with data on the M8 API as fired from aircraft. This was figure was published in the NDRC report Analytic Studies in Aerial War on page 105 https://www.loc.gov/resource/gdcmassbookdig.analyticalstudie02bush/?sp=123&st=image&r=-0.299,0.05,1.611,1.294,0 The Small Arms Development Report also contains a table, which gives the mean radius of dispersion of various 50 caliber ammunition in inches at 600 yards. At 600 yards 1 mil is = to 7.2 inches. Thus, the mean radius of dispersion can be computed for each of the bullets. As the mean radius of dispersion Inches / 7.2 = Mean Radius of Dispersion mils. https://archive.smallarmsreview.com/archive/detail.arc.entry.cfm?arcid=13265 Bullet Name Mean Radius of Dispersion at 600 yards in Inches Mean Radius of Dispersion Mils M8 API 12 1.666666667 M2 AP 50 Cal 10 1.388888889 M1 Incendiary 50 cal 12 1.666666667 M20 APIT Std Core 12 1.666666667 M23 Incendiary 50 12 1.666666667 M21 Headlight Tracer 20 2.777777778 Ball M2 50 Cal 9 1.25 M10 Tracer 50 Cal 20 2.777777778 The first edition of the “Fighter Gunner Manual” the dispersion is given. As has the dispersion listed as 100% 8 mil and 4 mil 75% This same graphic appears in the later manual. Air Force Manual 64 Fighter Gunnery https://archive.org/details/air-forces-manual-no.-64-fighter-gunnery-firing-rockets-dive-bombing-1-may-1945/page/66/mode/1up Boresight and alignment charts at the back of this manual confirm that almost every aircraft used by the Air Force during the war had a dispersion rating of 4 mil 75% eg 1.2 sigma. Meaning the 100% value was 8 mils. The P-51b shows the 75% dispersion is 4 mils as do all most all the fighter aircraft used by The Army Air Force at this time. 4 mil 75% / 8 mil 100% was still the standard in the 1950’s https://www.google.com/books/edition/AF_Manual/81krAQAAMAAJ?hl=en&gbpv=1&pg=PA155&printsec=frontcover All of this information seems to indicate the 100% dispersion circle for the 50 caliber is around 8 mils and therefore the value Da0 should be set closer to 0.001. If you made it this far, thanks for taking the time to read all this. In the next few posts I’ll be adding some more information and building some ballistic tables for various aircraft weapons.