Continuing our discussion from the file comments, I once again want to thank you for putting this together. Your and Reflected's work have really stirred my imagination and problem-solving drive. I've learned a ton from playing this mission, studying historical documents, and playing with your code. I have some insights and suggestions I want to share.
Bugs
The Report Results feature does nothing after the bombs landed. There is nothing unusual in dcs.log.
Feature Requests
Briefing should have both ground speed and indicated air speed with clear distinction between the two.
Swap the sign convention on the training aid so the range is negative if you're too close to the Cat station and positive if too far.
Add a rough function for bomb trail so the bombs land in the target zone. More on this below.
I would like to see how precisely I flew on the beam (RMS error about the Cat radius) and how close to the nominal parameters (beam distance, heading, speed, altitude, timing) my release was. It's possible to use the linearized equations below to see how each error contributed to how much the bombs missed.
It may be better to report the bomb results in along-track and cross-track components rather than polar coordinates.
Add an Air Start option near the 20-mile rally point so it's possible to get more practice.
Staying on beam
While on beam, use shallow bank (<10 degrees) to make course corrections of 2-5 degrees. Very little rudder is required for coordination because you are at cruise speed, but a brief tap is helpful to initiate yaw when banking. Avoid using pitch to initiate the turn because it will mess up your speed and altitude. Use the turn coordinator to ensure turns are consistent.
For a ground speed of 300 mph and a Cat radius of 100 miles, staying on beam means turning toward the Cat station at and average rate of 3 degrees per minute. This is 1/60th of a standard-rate turn and requires about half a degree of constant bank. While Mosquito pilots report being able to stay on beam using gentle pressure on the rudder, this might not be easy for the average sim player's hardware. I think the best beginning strategy is to bounce between the edges of the beam in straight and level flight. This is similar to how real pilots fly DME arcs.
The length of the longest possible straight path through an equisignal beam with width w and radius r is approximately 2*sqrt(2rw). For a 100 mile Cat radius and 32 meter beam width, this is 4 miles, or 48 seconds at 300 mph. One possible strategy for flying the beam is to bounce along its edges like a photon in an optical fiber. Fly in a straight line and make a 4 degree turn toward the Cat station every time you hear dashes and a 2 degree turn away from the Cat station every time you year dots. Adjust the turn heading if you go more than 30 seconds without the beam.
While in level flight, you are always being accelerated away from the Cat station in the rotating frame. This means you need less extreme course corrections to move away from the Cat station than to move toward it. While within the beam, try to compensate for this centripetal by making gentle turns of about 1 degree toward the Cat station every 10-20 seconds.
Accuracy
The basic equation for the travel distance of a projectile launched in a vacuum is:
where L is the along-track displacement of the projectile, v is the ground speed, and t is the time of flight.
The cross-track error T may be expressed according to the course error (delta_theta) and distance from the beam:
For a projectile in a vacuum, the time of flight may be expressed as
.
For a drop from 20,000 feet, the fall time is about 36 seconds. Therefore, the distance traveled is:
L = \frac{v}{g}\left (\sqrt{2hg+\dot{h}^2}+\dot{h}\right )\\
where g is the acceleration of gravity, h is the release height, and hdot is the vertical speed (which is much smaller than 2hg). This equation does not account for trail to to drag, but trail is normally only about 10% of the total distance traveled. This vacuum equation can be differentiated to explore the relationships between small errors in the release parameters and the impact point. So, if we differentiate L and T with respect to all six terms, we get the following approximate linearized relationship between the impact point and errors in the release parameters.
\Delta L = v\Delta t+ t\Delta v+\frac{v}{gt}\Delta h+\frac{v}{g}\Delta \dot{h}
The implications of these equations are that in order to get within 100 meters of the target, the Mosquito needs to release with six parameters matching their nominal values, in order of priority:
On beam
±2 mph of ground speed
±1 degree of course
±0.3 seconds of the release signal
±300 feet of altitude
±600 feet per minute of vertical speed
Speed, beam position, and course are the most critical. There's a ton of flexibility in altitude and vertical speed, meaning that the pilot should prioritize matching the correct ground speed at the release over altitude. The easiest way to get to a speed quickly is by changing pitch because gravity provides more acceleration than the engines. Good energy management on the flight path can ensure that speed and altitude are easily converted into an accurate shot. At 300 mph GS, 100 ft of excess altitude may be converted into 5 mph of speed while conserving energy.
Heading needs to be adjusted to the correct release heading by the dash on the 5T release signal. If you're steady on the beam, you should be close enough to the correct heading to have time to make this correction.
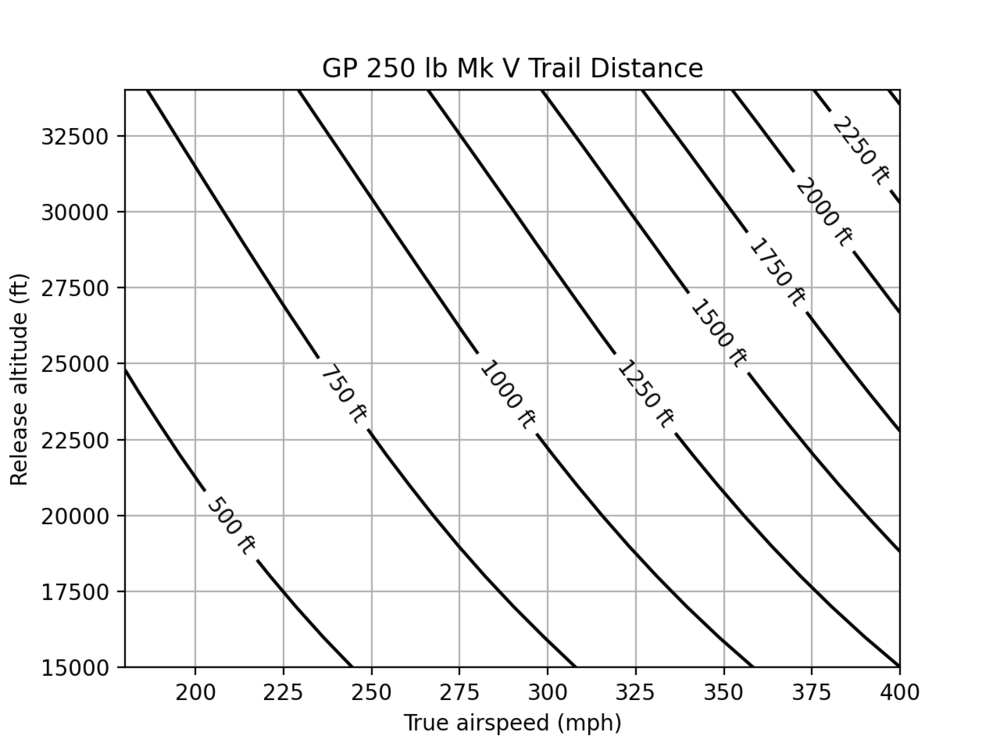
Bomb Trail Distance
I noticed in your script that the target zone was displaced from the nominal target because of the vacuum approximation. I did some simulations of the bomb's trajectory, using Tacview for calibration and found a good empirical function for trail distance. I modified the code and now I can get the bombs within 100 meters of the target.
I took at peek at the Lua files for WWII weapons and found the mass and frontal area of the GP 250 Lb Mk V. The cx_coeff line for the drag coefficient and its dependence on Mach number is inscrutable to me, so I had to to infer the drag coefficient using a least-squares fit to the vertical speed of the bomb as function of time. I generated a simulation of the bomb's trajectory using SciPy's odeint at various release heights and speeds. To find the drag coefficient, I also propagated a state transition matrix to linearly relate the initial parameters to small differences in these parameters as a function of time. I then used least-squares to fit these values to vertical velocities measured in Tacview, which gave me a good estimate of the modeled drag coefficient. My trajectories can predict the Tacview data within about 1 m/s. I used the Prandtl-Glauert factor to approximate the drag coefficient's dependence on Mach number.
With a good drag coefficient model in hand, I simulated trajectories for a range of of release heights and was able to generate contour plots of trail distance as a function of release altitude and speed. These functions were relatively smooth, so I fit a power law to them, which yielded this:
Forgive the unit system stew. This expression typically matches my simulations within 30 meters. Notice the near-linear dependence of the trail distance on altitude. This jives with the conventional wisdom that bombs fall at a constant trail angle that depends only on airspeed.
I added this formula to the Oboe script and then subtracted the trail distance from the release distance in the code. I can now get within 100 meters of the target, but I have yet to actually damage the ground unit.
oboe.lua OBOE_DEMO_DAY_quickmod.miz