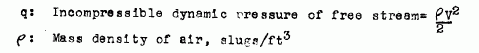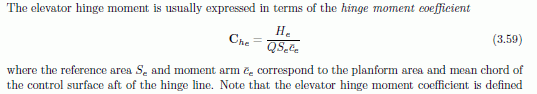effte

What happens to your required landing distance on grass? It goes up. What does this imply as for the friction on grass? You're mixing it up with the rolling resistance, which is something else entirely. Yes, one decreases and the other increases, and it is the reduced friction/increased slip angles which makes the difference as far as ground handling margin goes. Here you go for an idea about the relative friction coefficients: http://physics.info/friction/ Rough LDR calcs: http://www.chesapeakesportpilot.com/pages/hot_topics/grass_landings.pdf

These aircraft should handle landing on a grass field just fine. However, a grass field (as in grass strip) is not just any plain old field you happen to find. Land in an arbitrary field, and it is likely to end up in disaster. They will be too bumpy, causing you to get airborne again with too little airspeed. They will be too soft, causing the landing gear to dig in and the aircraft to nose over. The grass will not be maintained to the required standard, again likely causing too much drag and possibly a nose-over - and definitely problems taking off again, or perhaps even to get the aircraft rolling from a standstill. Piles of grass in front of the main tyres are rather effective shocks. Never brake to a stop on a grass field, especially if the grass hasn't been cut in the last few days... It's not increased friction which makes it easier to control conventional gear aircraft (taildraggers) on grass, but rather decreased friction. The lower (and quite different) friction allows a higher tyre slip angle (that's the sideways movement over a ground exhibited by any tyre which provides a force perpendicular to the direction in which it is rolling) for a given lateral force, which means you can get it more sideways before coming to grief. This translates into larger margins for error and much more forgiving ground handling. Cheers, /Fred

A track would be a good thing.

"Segmented modelling of the lifting surfaces", or suchlike. The wing itself isn't segmented, but the model treats it like segments. I very much agree that the sentence needs to be rewritten.

From the MiG-21Bis Flight Operating Instructin floating around: "The service ceiling for an aircraft carrying two missiles and climbing at FULL THROTTLE at a true airspeed of 870 km/h, is 12,000 m (under the standard atmosphere conditions, at an average weight of the aircraft) and 11,0000 m with four missiles. The service ceiling for an aircraft carrying two missiles and climbing at FULL REHEAT (under the standard atmosphere conditions) is 17,500 m, the fuel remainder at the ceiling altitude amounting to 700 l." The procedures to use are also described.

The props are meant to be able to take off and land on turf, and have corresponding relationships between tyre dimensions, aircraft weight and tyre pressure. Jets typically have immense tyre pressures, and accordingly sink to the axle if you try to taxi them outside of prepared surfaces. You need jacks to get them out. To give an idea, aircraft tyres can be akin to explosives going off when they burst, or if the rims come apart. It's a killer.

No difference. The PRMG gets you to where you (hopefully) can see the runway at 300 m or so (!). From there on, you proceed to land visually as per usual. If you can't see the runway, you wish really hard for more fuel than those 700 remaining. ;)

Going by the OP, high alpha isn't the issue as much as - as previously pointed out by Kuky and Buzzles - unloading (low/negative G). The fuel system in the MiG can't cope, so the engine flames out from fuel starvation. Just roll inverted and pull positive Gs. Tends to be less of an issue in real life, as you'd probably do that anyway just to save yourself the discomfort. DaveRindner, very nice explanation buty you're mixing compressor stalls and unstarts in the same description. It gets kind of muddy to follow. A compressor stall is when we ask too much from the compressor, making the blades stall. It can also be caused by disturbed airflow into the compressor face from e g high alpha or beta conditions. The stalled compressor allows the high pressure behind the compressor to go forward and out the inlet, with a loud bang and often flames. While it can cause a flameout, it typically doesn't. I can tell you from first-hand experience that it is something which will get your attention - and quickly. There you are, all cosy up in cruise, catching up on the paper work and - BANG BANG BANG BANG! :D An unstart is when we're trying to shove too much air down the inlet, more than the compressor can ingest. This causes the shockwave system inside the inlet, set up to deliver subsonic flow to the compressor face, to become all messed up. The normal shock (a shock perpendicular to the airflow, with supersonic flow on the upstream side and subsonic flow on the downstream side) moves forward and possibly even out of the inlet where what we really want is an oblique shockwave off the tip of the spike, with supersonic flow both up- and downstream of the shockwave. One can lead to another so you can have both at the same time, but they are different phenomena. I'd drop the analogy with breathing, and introducing stalled wings along with compressor stalls has been found to cause immense confusion. :) Cheers, /Fred

Really? http://www.sci.fi/~fta/migflt-2.htm http://www.mig-21.de/english/technicaldataequipment.htm

I just had a go in the current version, and 20k feet is, as it should be, not something the Mustang even breaks a sweat over. Due to the concerns about the current modelling of the oil system, I kept a higher than normal climb speed of 160 mph indicated all the way up and left the radiators fully open manually. Apart from that, 46"/2700 rpm got me there with a good rate of climb and no issues. If you prematurely shift the blower into high, you may be wasting horse power running the compressor. It's not needed - let the aircraft do it's thing and worry about maintaining proper air speed and manifold pressure. Try this, and if you still have issues describe how you are going about it and we'll see if we can nail the problem down. Cheers, /Fred Edit: Treat the above climb speed with a grain of caution - it was off the top of my head, and doesn't seem to agree with the manual speeds when I double checked. Always go by the book and not by what some geezer on the net tells you. Edit of the edit: D'oh, I'm used to flying Mustangs with the ASI in knots. :doh: Try 175 to 10,000, 170 to 20,000 and from then on 165. But 160 mph IAS works as well, obviously. :)

Are you following the manual and holding proper airspeeds for the climb? Failure to do so is a common mistake.

Having an IR mav lock on to the IR spot would be the same thing as the optical seeker locking on to any bright light source on the ground. Just that it is bright doesn't mean it is the thing to guide to.

It is. We're pretty much exclusively concerned about force response out in the real world, power levers being the obvious exception.

There is nothing about a tandem arrangement in itself making it inherently difficult to takeoff and land with - I should know, having a fair number of takeoffs and landings on them. There have been a number of aircraft with a tandem arrangement which had peculiar handling qualities, but that's something else. Then you have the case where both mains of a tandem arrangement are far from the CoG, typically to make room for a bomb bay, making rotation in the traditional sense impossible. The only aircraft I'm familiar with which featured swivelling mains is the B-52, and that's not due to the landing gear arrangement in itself.

For some reason, I had trouble viewing your track. It replayed differently each time. 10 m/s is a hefty crosswind in a P-51, 20 knots. You must do it right. From what I could see, you had no aileron into the wind? Start out with stick back and into the wind. As speed builds, to somewhat above normal take-off speed, relax back pressure to allow the tail to lift. Relax into-wind pressure as you feel the aircraft wanting to dip the upwind wing, but a slightly wing-low attitude into the wind is preferable to relaxing the control input too much. I'd say it's even desirable to dip the upwind wing, just a degree or three. Speed is your friend. Do not attempt the aircraft to take off for you until you have airspeed aplenty, at which point you decide to take off and make it so. Finally, ground handling still isn't an area where DCS shines. Once you get it sideways, it's Disney on Ice. As long as you keep the aircraft straight, it's OK by now. Acquire a visual reference point in the far field, a cloud or such, and work those pedals to keep it centered. The usual mistake when learning conventional gear is overcontrolling. You need a good amount of pedal to stop a developing swing, but once you've stopped it you have to relax pedal pressure before you see the nose start coming back, or perhaps even before you've arrested the swing completely, or you're setting yourself up for a swerve in the opposite direction. It is doable, but tricky. What are your frame rates like? Slow frame rates won't help a bit. I'm not sure if frame rate issues can cause track replay difficulties on the other end? Cheers, /Fred

Drag. Heaps of it.

Posting a track is always a good start. It makes it a whole lot easier to see what goes wrong. Rgds, /Fred

I posted the intercept profile by the book in another thread. Cheers, /Fred

Intercept profile by the book: Accelerate after start to reach 950 km/h TAS by 1000 m. Maintain TAS until 10,000 m. Accelerate to 1200 km/h IAS and maintain until M1.9, which is then used for the rest of the climb. The acceleration at 10,000 feels slow as molasses initially, but once past 1000 km/h the engine can breathe happily again and things start happening. Reheat from the get-go. Cheers, /Fred

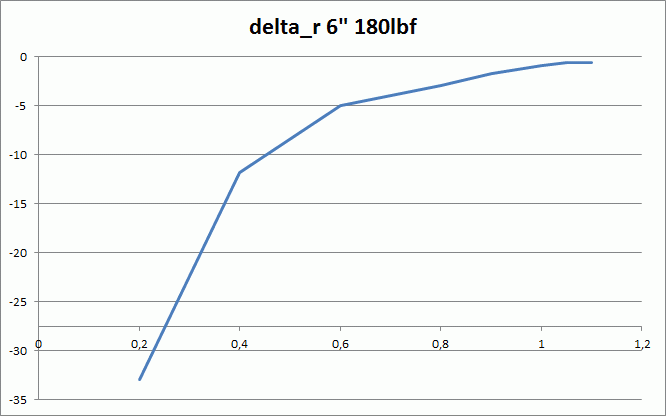
Indeed. First point of order would be to establish if the empirical rudder deflections achievable roughly match the calculated values. To get further, we need the documentation on the beta/delta_r relationship. I haven't got the time, but I put together a graph anyway assuming 6" pedal throw and 180 lbf available at the pedal. I don't know if I have much trust in the >=M1.0 values, and the available deflection at M.2 is an obvious extrapolation - force for full deflection calculated earlier to be less than 180 lbf.

First off, it is the greek character 'rho', not 'p'. Getting that right will save you a lot of confusion later on. Lowercase 'rho' is the standard designator for density, in aeronautics and pretty much everywhere else in science. Second, yes, q=rho*V^2/2 But you didn't try calculating q yourself, using your suggested figures, did you? Instead, you used the value you pulled off your lookup tables on the web - which, within the confines of numerical precision, is the same value I calculated and not what you would have arrived at. Now, didn't that quote suddenly get embarrassing? Yes, verification is a good thing, especially when relying on what google found you online. Oh, indeed? And as you used the same value, even though you suggested the wrong method of calculating it, that would make your calculations.... ? I also suggest a bit of reading. Start with your own references, conveniently repeated above. What are you on about? No, I won't even bother outlining why that's wrong. Read your own references for a change. The important bit is, as mentioned, reproduced in this very thread for your convenience (even though it seems to have turned into a bit of an inconvenience for you). Pedal forces or pedal moments about a defined point and with a defined moment arm. Choose one. And the rudder hinge moment for full deflection comes out to 540 lb-ft, as shown in my initial post. Glad we're in the same ballpark, finally. Show how you arrived at the figure of 505 lb-ft and we may be able to find the discrepancy. That would be about 2.5 times the recommended maximum force for normal operation at the pedals, and still far in exceedance of the maximum achievable force in a lab setting. What are you on about? No, you cannot skip the parentheses, as shown. Youthful enthusiasm shall normally be applauded and supported. I would have been all pedagogical, but your attitude in the forums and out of public view just zapped my desire to go the extra mile for you. I would leave you alone rather than spend my spare time administering physical violence to this particular deceased creature of equestrian nature, weren't it for the fact that some apparent traction had been gained by your attempt at providing seemingly credible 'evidence' for something being amiss. q = rho*V^2/2 Where rho is density kg/m^3 V is true airspeed m/s [q]=[rho][V^2]=kg/m^3 * m^2/s^2 = kg / (m s^2) F=ma gives [m]=[F/a]=N*s^2/m so [q] = N s^2 m/(m s^2) = N s^2 / (m^2 s^2) = N/m^2 That's for mass per volume. Go ahead and insert a moment per volume or force per volume, both of which you seem to be suggesting simultaneously, and see where it gets you. Did you actually read the links you provided? If you did, you're trying to pull a fast one and hoping no one else will read them. If you didn't, in your rush to google references to gain apparent credibility to your claims, well... I suggest you do so now. No, research is not done by googling convenient search terms, browsing through the hits for formulas, plugging in numbers according to TSABR and then posting the results liberally sprinkled with links for faux credibility. The important bit is reading and understanding the references you find and decide to use. Yes, it is an unfortunate fact of life that this will take a lot more effort. I think I'm done here, so save yourself the trouble of replying. It would at this point be very interesting to find data on the relationship between beta angle and rudder deflection. With that, we'd know exactly what is correct, as far as rudder efficiency goes. I suspect the devs have that information available. Perhaps a reference could be provided in order to settle that part of the discussion?

Did those two types have a reputation for being difficult? There's nothing inherently difficult about a tandem gear arrangement in itself. Depending on the exact design, the procedures can be somewhat unconventional though (but not unique). Cheers, /Fred

Posting in a hurry before coffee? :) No, crossed controls after takeoff and on climbout is a Bad Idea and surely not what Crumpp intended to post. After takeoff, you let the aircraft yaw (crab) into the wind and keep the wings level for the climbout. The book linked seems a good one at a quick glance (thanks for the link) and you will find it in agreement. Cheers, /Fred

And those altitudes aren't difficult to achieve, if you fly a profile by the book.

Curly, it is always interesting to have an open discussion between adults. It is much better than arguing with kids who throw a hissy fit and negrep those who question their statements. I was hoping for the former. I am also relieved too see that I'm not the only one who finds your rather unorthodox take on algebra hard to follow. Somewhere in your flurry of edits you wrote that I was using the wrong formula when, in fact, it is the exact same formula you used for your calculations (as opposed to the one you posted, which I had to correct). Getting the base facts straight Rudder hinge moment C_Hr = H / (q*s_r * c_r) (1) Note the parentheses. Note the word "movable" in the above definitions. And while we're at it, Finally, for the vertical tail: (All from AD069271/NA-50-1277). Oh, and your second reference... What's the magic word there? The formula derived From (1) C_Hr = H / (q*s_aft * c_aft) => H = C_Hr * q * s_aft * c_aft I'll let you figure out the slugs and dynamic pressures on your own - you'll get there, just keep at it. Where it all went wrong, and your plan just fell apart... (to paraphrase a good song!) Where you went wrong was using the MAC for the entire vertical tail (sort of, you converted it correctly to 4.665 ft and then used 4.65 instead for your calculations) times the rudder area, instead of the area moment conveniently presented to you by the good people at North American. Humble pie time! But just a small slice, thank you. I take it you have no reference at all for the 6" of pedal travel? Well, let's use it anyway. And here, you are right - I miscalculated the mechanical advantage. That's what you get for rushing. Hinge moment = force * moment arm. For 27.5° of travel to result in 6" of movement, assuming a rigging arrangement converting the rotation to linear motion with a linear relationship between deflection of the rudder and the pedal, the moment arm r can be found through 27.5°/180°*pi*r=6" r= 6"*180°/(27.5°*pi) = 12.5" = 1.04' In other words, the pedal force is the hinge moment divided by 1.04, based on the specified assumption of ft-lbs. The formula google had found you used in-lbs. It is unfortunate that the AD069871 report does not specify the unit. There's another unit ambiguity in that they specify the average cord aft of the hinge line to be in inches, but specify the area moment in ft^3. If the moment is in in-lb, then your mechanical advantage calculations are correct - but then it stands to reason that the control surface average cord aft of the hinge line is indeed in inches, as specified, and we have to multiply the given area moment by 12. Net result: My figures. Sanity check The xwind landing case would likely be the design constraint used for the rudder system. For a sanity check let us use 132 KTAS and see if full deflection of the rudder will give us a pedal force which is in the ballpark and not a factor 12 off. Thats, again, conveniently M.20 (225 ft/s) so C_Hr = .265 at 0° yaw. H = C_Hr * q * s_aft * c_aft = .265 * (.00237*225^2/2) * 9.72 = 154 ft-lbs. With mechanical advantage, 154/1.04 = 148 lfb at the pedal. If we instead assume a hinge moment in in-lbs, we must assume that the rudder average chord aft of the hinge line is also to be specified in in rather than ft, giving H = C_Hr * q * s_aft * c_aft = .265 * (.00237*225^2/2) * 9.72*12 = 1854 in-lbs. Then, your mechanical advantage calculation is correct and we get a pedal force of 1854/12.5 = 148 lbf. What a peculiar coincidence! The pedal force required for full rudder deflection at the recommended limiting crosswind is almost spot on the pedal force deemed manageable by the FAA. Loose ends As for the fin, we can discuss that when you stop using pounds of hinge moment as a force to make some kind of point. Or maybe not. Your link on reversible control systems references rather interesting figures on rudder pedal forces as well. Whaddya know, 150 lbf. Now, how can this be? In the lab, 300-400 lbf from test subjects, yet the regs call for 150 lbf - written down from a previous figure of 180 lbf? The thing is: You cannot satisfactorily fly an aircraft while exerting all the force you can muster on a pedal. Test pilots would not sign off on a xwind capability requiring them to strain until they turn blue on short final, and the mapping between the maximum deflection of our Saiteks and the control force applied by our virtual alter egos should not mimic such a lab value - unrealistic in every day operations. As for the book you're such a big fan of, read your quote. Assuming you are quoting it correctly, isn't there a thing or two which seems a bit peculiar right there? The lecture slides you linked had those "huh?" moments liberally sprinkled throughout the text, for anyone to find. Where is it used for undergrad training? If the slides based on it are representative, that's job security for the old hands in the industry right there. Can you find anything peculiar in the image you posted? More pie, and an exercise for the avid reader I did make a mistake in calculating the crab angle, resulting in an error of almost -0.2°. Can you spot it? Whoooosh I'm afraid the high school physics weren't exactly the answer to the point I was making. Summary I don't think you present much of a case for anything to be changed. Does this mean I believe everything is fine with the model? Nope, nor do I claim to have found anything wrong. Flat turns should be possible, and they weren't really a while ago. OTOH, they have very limited practical use. As long as I can de-crab and sideslip, I'm a happy camper. The latter would obviously be affected if the lateral forces due to beta angle are off (or missing), but I haven't done the testing to see if anything is really amiss.